Question Number 97439 by bemath last updated on 08/Jun/20
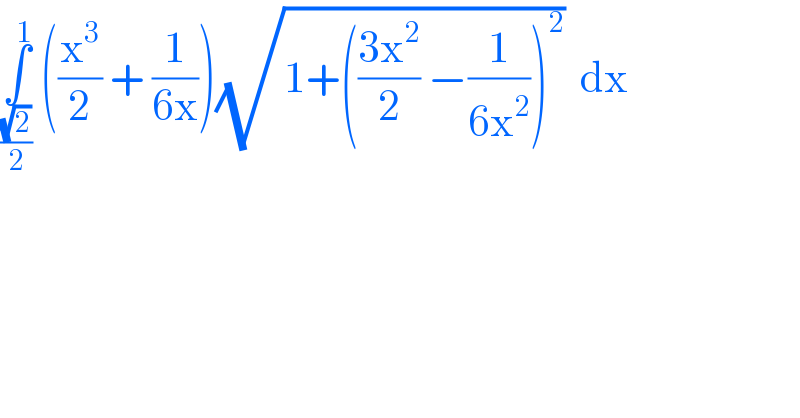
$$\underset{\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}} {\overset{\mathrm{1}} {\int}}\:\left(\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{2}}\:+\:\frac{\mathrm{1}}{\mathrm{6x}}\right)\sqrt{\mathrm{1}+\left(\frac{\mathrm{3x}^{\mathrm{2}} }{\mathrm{2}}\:−\frac{\mathrm{1}}{\mathrm{6x}^{\mathrm{2}} }\right)^{\mathrm{2}} }\:\:\mathrm{dx} \\ $$
Commented by john santu last updated on 08/Jun/20
![(1) 1+(((3x^2 )/2)−(1/(6x^2 )))^2 = 1+((9x^4 )/4)−(1/2)+(1/(36x^4 )) =((9x^4 )/4)+(1/2)+(1/(36x^4 )) = (((3x^2 )/2)+(1/(6x^2 )))^2 (2)(√(1+(((3x^2 )/2)−(1/(6x^2 )))^2 ))= (√((((3x^2 )/2)+(1/(6x^2 )))^2 )) = ((3x^2 )/2)+(1/(6x^2 )) (3)∫_((√2)/2) ^1 ((x^3 /2)+(1/(6x)))(((3x^2 )/2)+(1/(6x^2 ))) dx = ∫_((√2)/2) ^1 (((3x^5 )/4)+(x/3)+(1/(36x^3 ))) dx = [ (x^6 /8)+(x^2 /6)−(1/(72x^2 )) ]_((√2)/2) ^1 = (1/8)(1−(1/8))+(1/6)(1−(1/2))−(1/(72))(1−2) = (7/(64))+(1/(12))+(1/(72)) = (7/(64))+(7/(72)) = ((63+56)/(576)) = ((119)/(576)) ∴](https://www.tinkutara.com/question/Q97442.png)
$$\left(\mathrm{1}\right)\:\mathrm{1}+\left(\frac{\mathrm{3x}^{\mathrm{2}} }{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{6x}^{\mathrm{2}} }\right)^{\mathrm{2}} =\:\mathrm{1}+\frac{\mathrm{9x}^{\mathrm{4}} }{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{36x}^{\mathrm{4}} } \\ $$$$=\frac{\mathrm{9x}^{\mathrm{4}} }{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{36x}^{\mathrm{4}} }\:=\:\left(\frac{\mathrm{3x}^{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{6x}^{\mathrm{2}} }\right)^{\mathrm{2}} \\ $$$$\left(\mathrm{2}\right)\sqrt{\mathrm{1}+\left(\frac{\mathrm{3x}^{\mathrm{2}} }{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{6x}^{\mathrm{2}} }\right)^{\mathrm{2}} }=\:\sqrt{\left(\frac{\mathrm{3x}^{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{6x}^{\mathrm{2}} }\right)^{\mathrm{2}} } \\ $$$$=\:\frac{\mathrm{3x}^{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{6x}^{\mathrm{2}} } \\ $$$$\left(\mathrm{3}\right)\underset{\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}} {\overset{\mathrm{1}} {\int}}\:\left(\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{6x}}\right)\left(\frac{\mathrm{3x}^{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{6x}^{\mathrm{2}} }\right)\:\mathrm{dx}\:= \\ $$$$\underset{\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}} {\overset{\mathrm{1}} {\int}}\:\left(\frac{\mathrm{3x}^{\mathrm{5}} }{\mathrm{4}}+\frac{\mathrm{x}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{36x}^{\mathrm{3}} }\right)\:\mathrm{dx}\:=\: \\ $$$$\left[\:\frac{\mathrm{x}^{\mathrm{6}} }{\mathrm{8}}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{6}}−\frac{\mathrm{1}}{\mathrm{72x}^{\mathrm{2}} }\:\right]_{\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}} ^{\mathrm{1}} \: \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{8}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{8}}\right)+\frac{\mathrm{1}}{\mathrm{6}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)−\frac{\mathrm{1}}{\mathrm{72}}\left(\mathrm{1}−\mathrm{2}\right) \\ $$$$=\:\frac{\mathrm{7}}{\mathrm{64}}+\frac{\mathrm{1}}{\mathrm{12}}+\frac{\mathrm{1}}{\mathrm{72}}\:=\:\frac{\mathrm{7}}{\mathrm{64}}+\frac{\mathrm{7}}{\mathrm{72}} \\ $$$$=\:\frac{\mathrm{63}+\mathrm{56}}{\mathrm{576}}\:=\:\frac{\mathrm{119}}{\mathrm{576}}\:\therefore\: \\ $$
Commented by bemath last updated on 08/Jun/20

$$\mathrm{thank}\:\mathrm{you}\: \\ $$
