Question Number 124203 by n0y0n last updated on 01/Dec/20
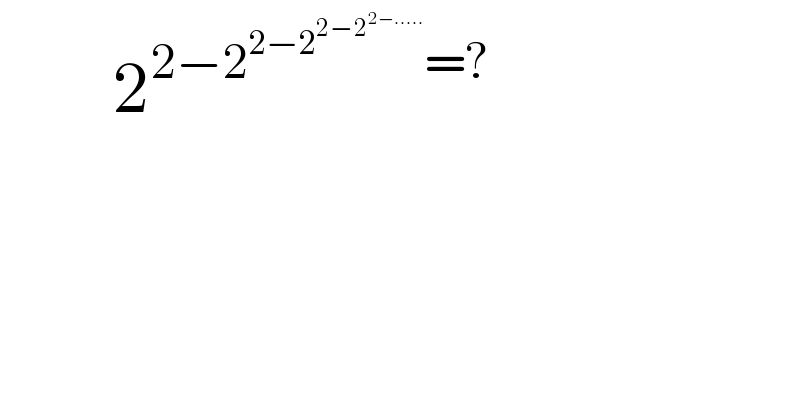
$$\:\:\:\:\:\:\:\:\mathrm{2}^{\mathrm{2}−\mathrm{2}^{\mathrm{2}−\mathrm{2}^{\mathrm{2}−\mathrm{2}^{\mathrm{2}−…..} } } =?} \\ $$
Commented by n0y0n last updated on 01/Dec/20

$$\:\mathrm{pls}\:\mathrm{details} \\ $$
Commented by MJS_new last updated on 01/Dec/20

$$\mathrm{it}'\mathrm{s}\:\mathrm{not}\:\mathrm{an}\:\mathrm{answer},\:\mathrm{this}\:\mathrm{user}\:\mathrm{is}\:\mathrm{not}\:\mathrm{able}\:\mathrm{to} \\ $$$$\mathrm{post}\:\mathrm{his}\:\mathrm{own}\:\mathrm{questions}… \\ $$
Commented by Ar Brandon last updated on 01/Dec/20
��
Answered by MJS_new last updated on 01/Dec/20

$${x}=\mathrm{2}^{\mathrm{2}−\mathrm{2}^{\mathrm{2}−\mathrm{2}^{…} } } \\ $$$$\mathrm{ln}\:{x}\:=\left(\mathrm{2}−{x}\right)\mathrm{ln}\:\mathrm{2} \\ $$$$\mathrm{let}\:{t}=\frac{\mathrm{ln}\:{x}}{\mathrm{ln}\:\mathrm{2}} \\ $$$$\mathrm{2}^{{t}} +{t}−\mathrm{2}=\mathrm{0} \\ $$$$\mathrm{approximating}\:\mathrm{I}\:\mathrm{get}\:{t}\approx.\mathrm{543000440865} \\ $$$$\Rightarrow\:{x}\approx\mathrm{1}.\mathrm{45699955913} \\ $$
Answered by mr W last updated on 01/Dec/20

$${x}=\mathrm{2}^{\mathrm{2}−{x}} \\ $$$${x}\mathrm{2}^{{x}} =\mathrm{2}^{\mathrm{2}} \\ $$$${xe}^{{x}\mathrm{ln}\:\mathrm{2}} =\mathrm{4} \\ $$$${x}\mathrm{ln}\:\mathrm{2}{e}^{{x}\mathrm{ln}\:\mathrm{2}} =\mathrm{4ln}\:\mathrm{2} \\ $$$${x}\mathrm{ln}\:\mathrm{2}={W}\left(\mathrm{4ln}\:\mathrm{2}\right) \\ $$$$\Rightarrow{x}=\frac{{W}\left(\mathrm{4ln}\:\mathrm{2}\right)}{\mathrm{ln}\:\mathrm{2}}\approx\mathrm{1}.\mathrm{457} \\ $$
