Menu Close

2-2-2-2-help-me-

Tinku Tara 0 Comments
Pin




Question Number 99256 by student work last updated on 19/Jun/20
(√2)^((√2)^((√2)^((√2) .....) ) ) =? help me
$$\sqrt{\mathrm{2}}\:^{\sqrt{\mathrm{2}}\:^{\sqrt{\mathrm{2}}\:^{\sqrt{\mathrm{2}}\:…..} } } =?\:\mathrm{help}\:\mathrm{me} \\ $$
Answered by mr W last updated on 19/Jun/20
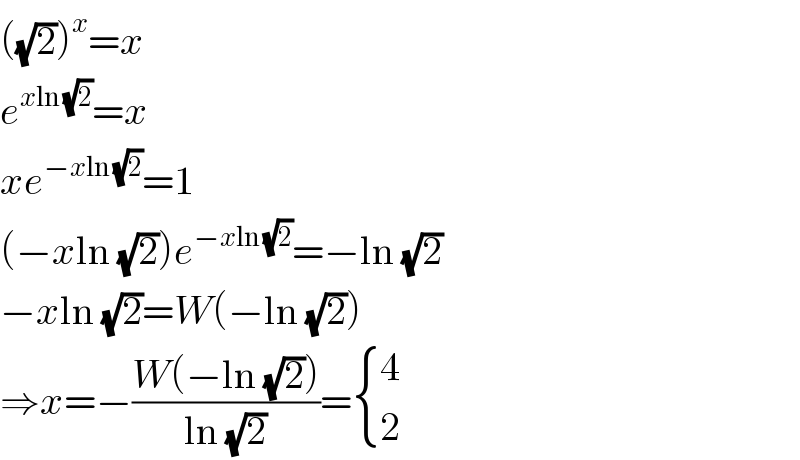
((√2))^x =x e^(xln (√2)) =x xe^(−xln (√2)) =1 (−xln (√2))e^(−xln (√2)) =−ln (√2) −xln (√2)=W(−ln (√2)) ⇒x=−((W(−ln (√2)))/(ln (√2)))= { (4),(2) :}
$$\left(\sqrt{\mathrm{2}}\right)^{{x}} ={x} \\ $$$${e}^{{x}\mathrm{ln}\:\sqrt{\mathrm{2}}} ={x} \\ $$$${xe}^{−{x}\mathrm{ln}\:\sqrt{\mathrm{2}}} =\mathrm{1} \\ $$$$\left(−{x}\mathrm{ln}\:\sqrt{\mathrm{2}}\right){e}^{−{x}\mathrm{ln}\:\sqrt{\mathrm{2}}} =−\mathrm{ln}\:\sqrt{\mathrm{2}} \\ $$$$−{x}\mathrm{ln}\:\sqrt{\mathrm{2}}={W}\left(−\mathrm{ln}\:\sqrt{\mathrm{2}}\right) \\ $$$$\Rightarrow{x}=−\frac{{W}\left(−\mathrm{ln}\:\sqrt{\mathrm{2}}\right)}{\mathrm{ln}\:\sqrt{\mathrm{2}}}=\begin{cases}{\mathrm{4}}\\{\mathrm{2}}\end{cases} \\ $$
Commented by 1549442205 last updated on 20/Jun/20
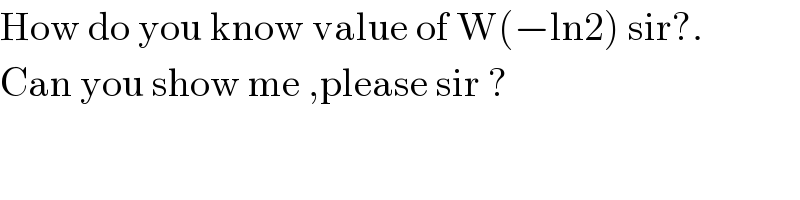
How do you know value of W(−ln2) sir?. Can you show me ,please sir ?
$$\mathrm{How}\:\mathrm{do}\:\mathrm{you}\:\mathrm{know}\:\mathrm{value}\:\mathrm{of}\:\mathrm{W}\left(−\mathrm{ln2}\right)\:\mathrm{sir}?. \\ $$$$\mathrm{Can}\:\mathrm{you}\:\mathrm{show}\:\mathrm{me}\:,\mathrm{please}\:\mathrm{sir}\:? \\ $$
Commented by mr W last updated on 20/Jun/20
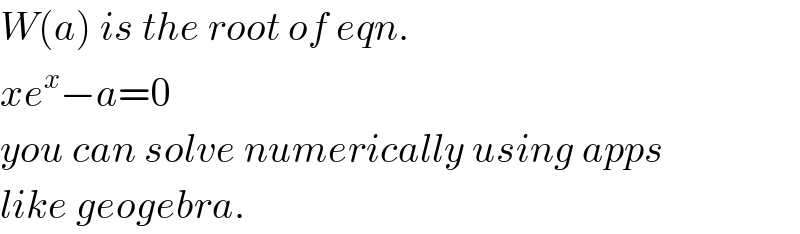
W(a) is the root of eqn. xe^x −a=0 you can solve numerically using apps like geogebra.
$${W}\left({a}\right)\:{is}\:{the}\:{root}\:{of}\:{eqn}. \\ $$$${xe}^{{x}} −{a}=\mathrm{0} \\ $$$${you}\:{can}\:{solve}\:{numerically}\:{using}\:{apps} \\ $$$${like}\:{geogebra}. \\ $$
Commented by student work last updated on 20/Jun/20
what means w sir?
$$\mathrm{what}\:\mathrm{means}\:\mathrm{w}\:\mathrm{sir}? \\ $$
Commented by mr W last updated on 20/Jun/20
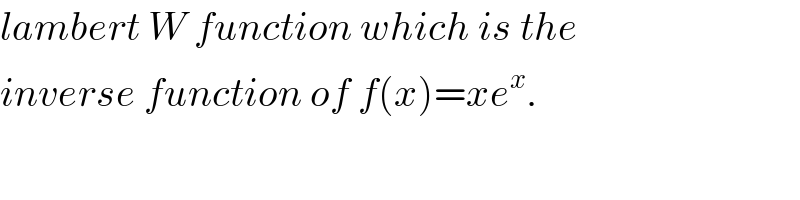
lambert W function which is the inverse function of f(x)=xe^x .
$${lambert}\:{W}\:{function}\:{which}\:{is}\:{the} \\ $$$${inverse}\:{function}\:{of}\:{f}\left({x}\right)={xe}^{{x}} . \\ $$
Commented by I want to learn more last updated on 20/Jun/20
Sir, we can use casio scuentific calculator too.
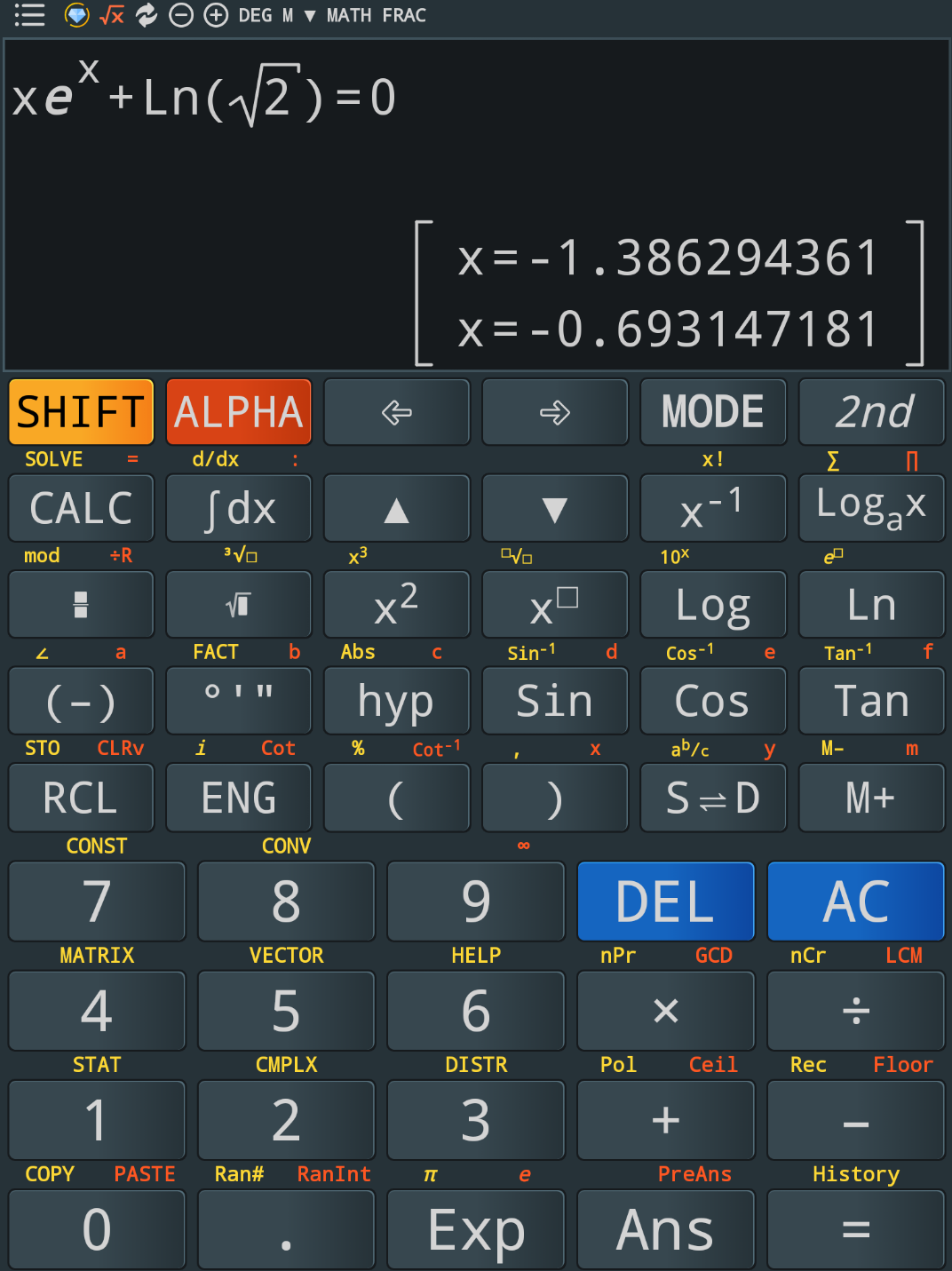
$$\mathrm{Sir},\:\mathrm{we}\:\mathrm{can}\:\mathrm{use}\:\mathrm{casio}\:\mathrm{scuentific}\:\mathrm{calculator}\:\mathrm{too}. \\ $$
Commented by mr W last updated on 20/Jun/20
fine.
$${fine}. \\ $$
Commented by I want to learn more last updated on 20/Jun/20
Commented by mr W last updated on 20/Jun/20
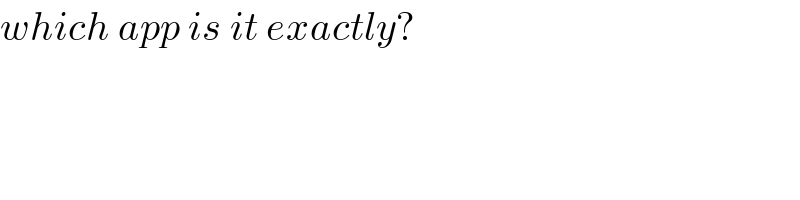
which app is it exactly?
$${which}\:{app}\:{is}\:{it}\:{exactly}? \\ $$
Commented by I want to learn more last updated on 20/Jun/20
sir it is casio fx 991 ex plus. Check play store sir. you can see casio business ..etc .. they are all the same.
$$\mathrm{sir}\:\mathrm{it}\:\mathrm{is}\:\mathrm{casio}\:\mathrm{fx}\:\mathrm{991}\:\mathrm{ex}\:\mathrm{plus}. \\ $$$$\mathrm{Check}\:\mathrm{play}\:\mathrm{store}\:\mathrm{sir}.\:\mathrm{you}\:\mathrm{can}\:\mathrm{see}\:\:\mathrm{casio}\:\mathrm{business}\:..\mathrm{etc}\:.. \\ $$$$\mathrm{they}\:\mathrm{are}\:\mathrm{all}\:\mathrm{the}\:\mathrm{same}. \\ $$
Commented by mr W last updated on 20/Jun/20
thanks! but i can′t find this app in play store.
$${thanks}!\:{but}\:{i}\:{can}'{t}\:{find}\:{this}\:{app}\:{in} \\ $$$${play}\:{store}. \\ $$
Commented by I want to learn more last updated on 20/Jun/20
Commented by I want to learn more last updated on 20/Jun/20
Sir, the first one. See what i searched
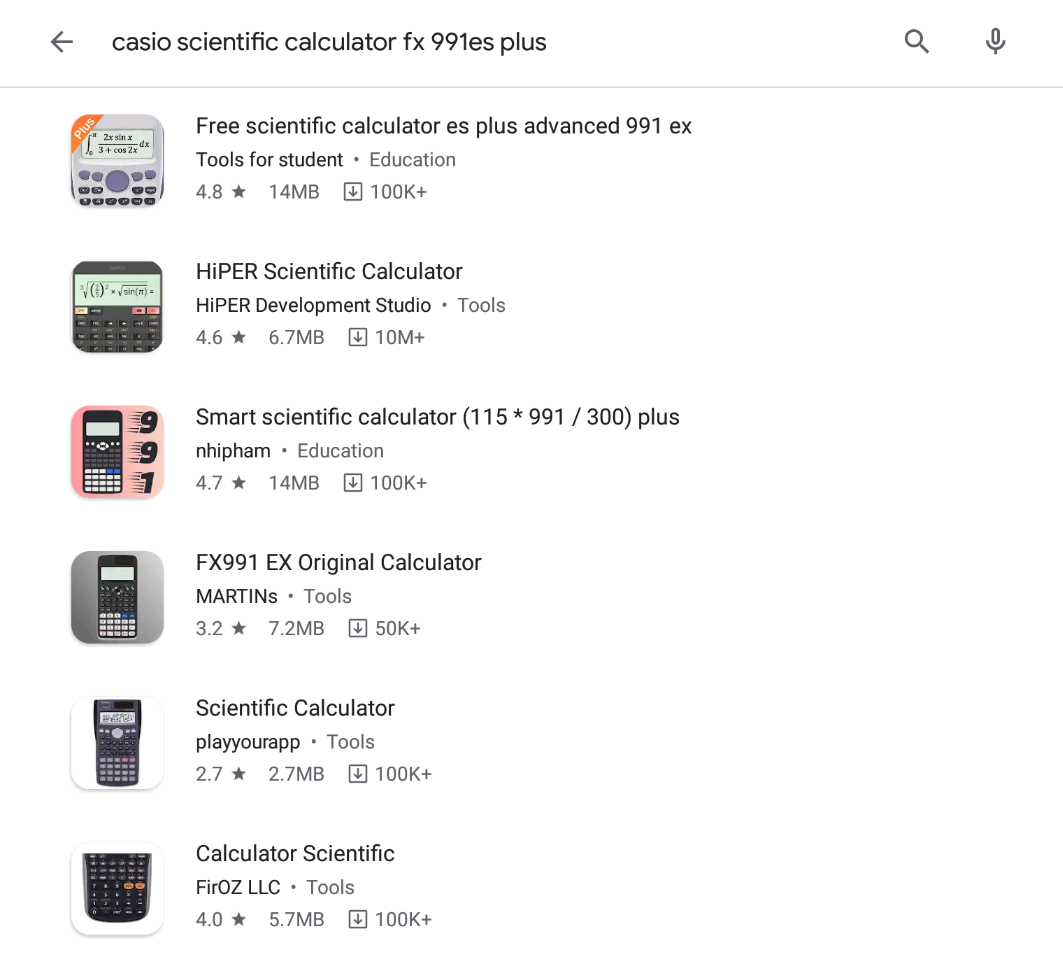
$$\mathrm{Sir},\:\mathrm{the}\:\mathrm{first}\:\mathrm{one}.\:\mathrm{See}\:\mathrm{what}\:\mathrm{i}\:\mathrm{searched} \\ $$
Commented by mr W last updated on 20/Jun/20
thanks again! i′ll try it.
$${thanks}\:{again}!\:{i}'{ll}\:{try}\:{it}. \\ $$
Commented by I want to learn more last updated on 20/Jun/20
Commented by I want to learn more last updated on 20/Jun/20
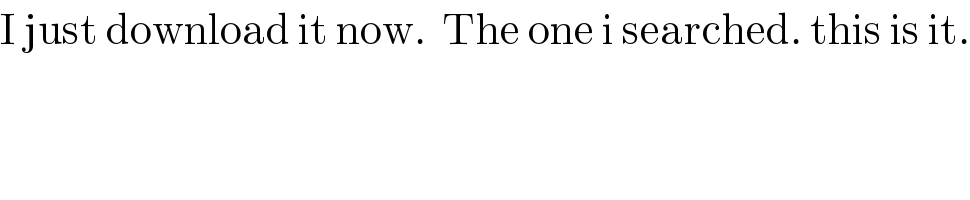
I just download it now. The one i searched. this is it.
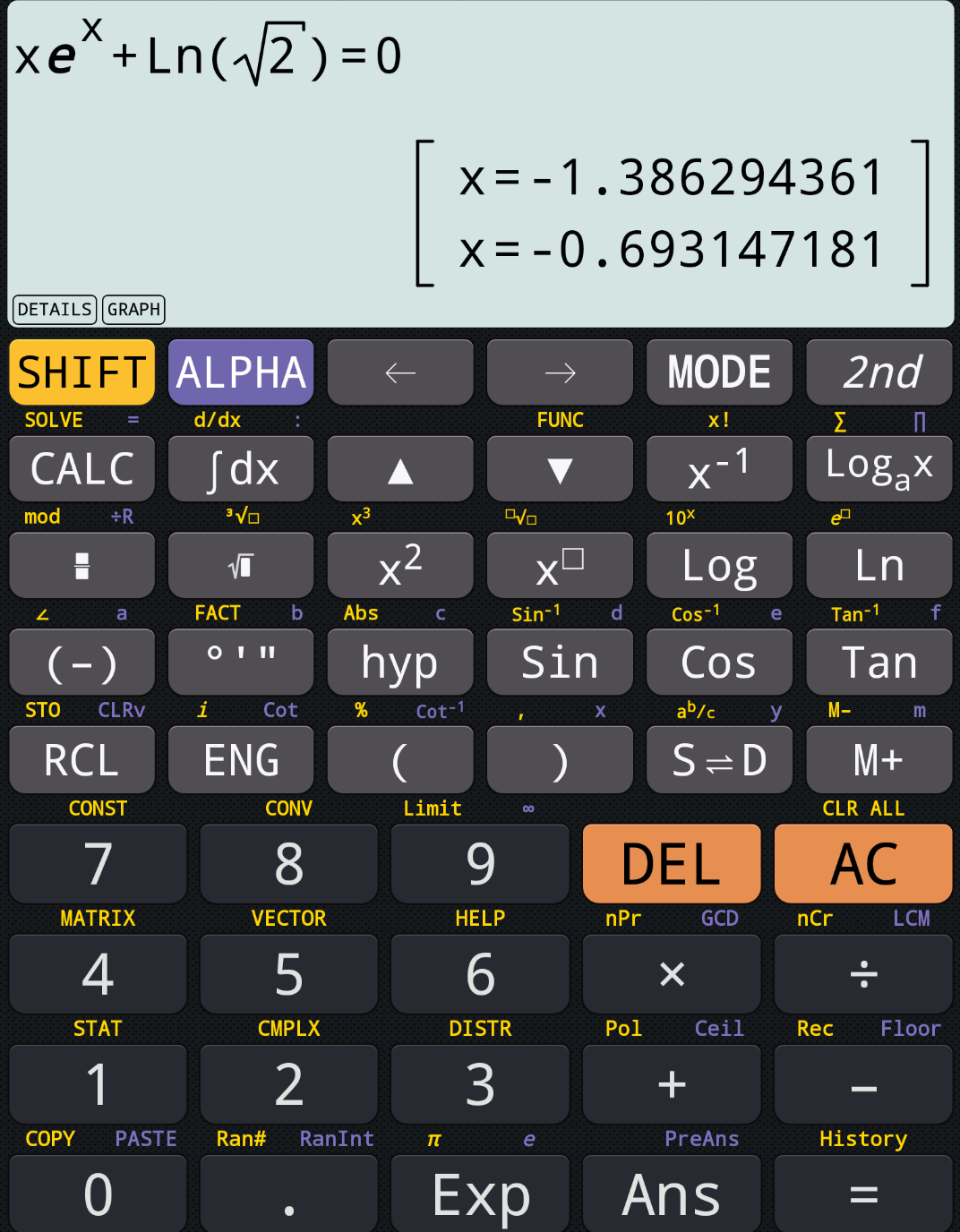
$$\mathrm{I}\:\mathrm{just}\:\mathrm{download}\:\mathrm{it}\:\mathrm{now}.\:\:\mathrm{The}\:\mathrm{one}\:\mathrm{i}\:\mathrm{searched}.\:\mathrm{this}\:\mathrm{is}\:\mathrm{it}. \\ $$
Commented by I want to learn more last updated on 20/Jun/20
the updated version . this one show graphs. And it is an offline calculator.
$$\mathrm{the}\:\mathrm{updated}\:\mathrm{version}\:.\:\mathrm{this}\:\mathrm{one}\:\mathrm{show}\:\mathrm{graphs}. \\ $$$$\mathrm{And}\:\mathrm{it}\:\mathrm{is}\:\mathrm{an}\:\mathrm{offline}\:\mathrm{calculator}. \\ $$
Commented by mr W last updated on 20/Jun/20
it seems to be powerful. i need some time to study its usage.
$${it}\:{seems}\:{to}\:{be}\:{powerful}.\:{i}\:{need}\:{some} \\ $$$${time}\:{to}\:{study}\:{its}\:{usage}. \\ $$
Commented by I want to learn more last updated on 20/Jun/20
It is a great calculator sir. I use the handling version in school. This is the phone version
$$\mathrm{It}\:\mathrm{is}\:\mathrm{a}\:\mathrm{great}\:\mathrm{calculator}\:\mathrm{sir}. \\ $$$$\mathrm{I}\:\mathrm{use}\:\mathrm{the}\:\mathrm{handling}\:\mathrm{version}\:\mathrm{in}\:\mathrm{school}. \\ $$$$\mathrm{This}\:\mathrm{is}\:\mathrm{the}\:\mathrm{phone}\:\mathrm{version} \\ $$
Commented by 1549442205 last updated on 21/Jun/20
Thank you sir.Yes,version N−cal on playstore
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir}.\mathrm{Yes},\mathrm{version}\:\mathrm{N}−\mathrm{cal}\:\mathrm{on}\:\mathrm{playstore} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *