Question Number 148043 by mathdanisur last updated on 25/Jul/21
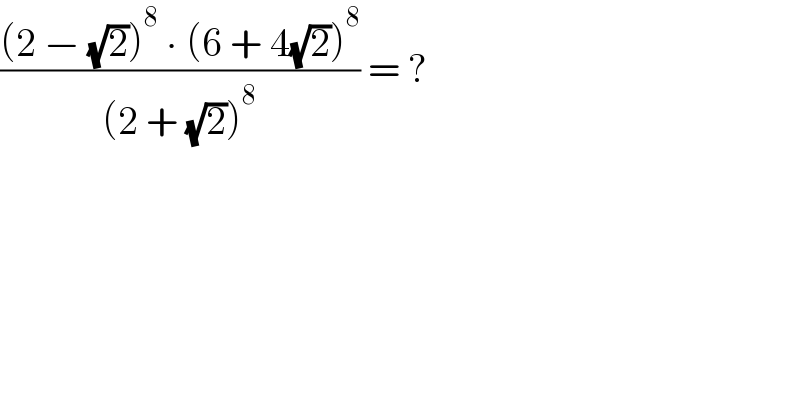
$$\frac{\left(\mathrm{2}\:−\:\sqrt{\mathrm{2}}\right)^{\mathrm{8}} \:\centerdot\:\left(\mathrm{6}\:+\:\mathrm{4}\sqrt{\mathrm{2}}\right)^{\mathrm{8}} }{\left(\mathrm{2}\:+\:\sqrt{\mathrm{2}}\right)^{\mathrm{8}} }\:=\:? \\ $$
Answered by iloveisrael last updated on 25/Jul/21
![[ (((2−(√2))(6+4(√2)))/(2+(√2))) ]^8 = [ (((2−(√2))^2 2(3+2(√2)))/2)]^8 = [(6−4(√2) )(3+2(√2) )]^8 = [ 2(3−2(√2))(3+2(√2))]^8 = 2^8 (9−8)= 2^8](https://www.tinkutara.com/question/Q148096.png)
$$\left[\:\frac{\left(\mathrm{2}−\sqrt{\mathrm{2}}\right)\left(\mathrm{6}+\mathrm{4}\sqrt{\mathrm{2}}\right)}{\mathrm{2}+\sqrt{\mathrm{2}}}\:\right]^{\mathrm{8}} \: \\ $$$$=\:\left[\:\frac{\left(\mathrm{2}−\sqrt{\mathrm{2}}\right)^{\mathrm{2}} \mathrm{2}\left(\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\right)}{\mathrm{2}}\right]^{\mathrm{8}} \\ $$$$=\:\left[\left(\mathrm{6}−\mathrm{4}\sqrt{\mathrm{2}}\:\right)\left(\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\:\right)\right]^{\mathrm{8}} \\ $$$$=\:\left[\:\mathrm{2}\left(\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}\right)\left(\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\right)\right]^{\mathrm{8}} \\ $$$$=\:\mathrm{2}^{\mathrm{8}} \:\left(\mathrm{9}−\mathrm{8}\right)=\:\mathrm{2}^{\mathrm{8}} \\ $$
Commented by iloveisrael last updated on 25/Jul/21
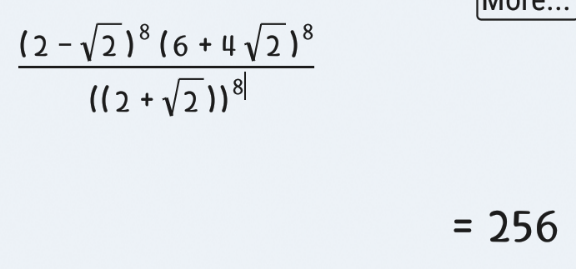
Commented by mathdanisur last updated on 25/Jul/21

$${Thank}\:{you}\:{Sir} \\ $$
