Question Number 117460 by Dwaipayan Shikari last updated on 11/Oct/20

$$\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{9801}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(\mathrm{4}{n}\right)!\left(\mathrm{1103}+\mathrm{26390}{n}\right)}{\left({n}!\right)^{\mathrm{4}} \mathrm{396}^{\mathrm{4}{n}} }=\frac{\mathrm{1}}{\pi}\:\:\:\left({Prove}\:{that}\right) \\ $$
Commented by Dwaipayan Shikari last updated on 11/Oct/20

$${This}\:{had}\:{been}\:{done}\:{by}\:{Ramanujan}.\:{Do}\:{you}\:{have}\:{any}\:{idea} \\ $$$${how}\:{to}\:{solve}\:{it}? \\ $$
Commented by mindispower last updated on 11/Oct/20
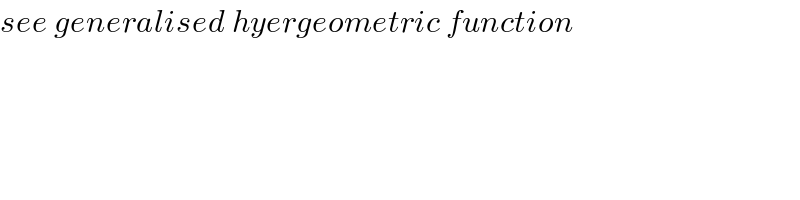
$${see}\:{generalised}\:{hyergeometric}\:{function} \\ $$
