Question Number 176188 by gloriousman last updated on 14/Sep/22
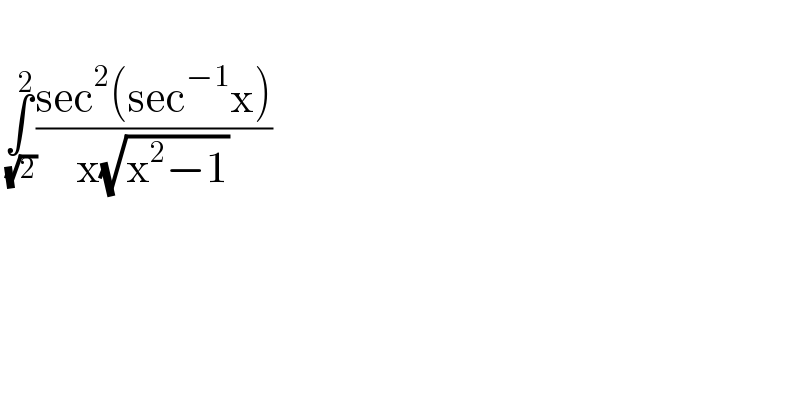
$$ \\ $$$$\underset{\:\sqrt{\mathrm{2}}} {\overset{\mathrm{2}} {\int}}\frac{\mathrm{sec}^{\mathrm{2}} \left(\mathrm{sec}^{−\mathrm{1}} \mathrm{x}\right)}{\mathrm{x}\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}} \\ $$$$ \\ $$
Answered by BaliramKumar last updated on 14/Sep/22
![∫_( (√2)) ^2 ((sec^2 (sec^(−1) x))/(x(√(x^2 −1))))dx let sec^(−1) (x) = y, when x = (√2) then y = (π/4) (dx/(x(√(x^2 −1)))) = dy, when x = 2 then y = (π/3) ∫_( (√2)) ^2 ((sec^2 (sec^(−1) x))/(x(√(x^2 −1))))dx = ∫_(π/4) ^(π/3) sec^2 (y)∙dy = [tan(y)]_(π/4) ^(π/3) = tan((π/3)) − tan((π/4)) = (√3) − 1](https://www.tinkutara.com/question/Q176196.png)
$$\underset{\:\sqrt{\mathrm{2}}} {\overset{\mathrm{2}} {\int}}\frac{\mathrm{sec}^{\mathrm{2}} \left(\mathrm{sec}^{−\mathrm{1}} \mathrm{x}\right)}{\mathrm{x}\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}}{dx} \\ $$$${let}\:\:\:{sec}^{−\mathrm{1}} \left({x}\right)\:=\:{y},\:\:\:{when}\:\:{x}\:=\:\sqrt{\mathrm{2}}\:\:{then}\:\:{y}\:=\:\frac{\pi}{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\frac{{dx}}{{x}\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}\:=\:{dy},\:\:{when}\:\:\:\:\:{x}\:=\:\mathrm{2}\:\:\:{then}\:\:\:{y}\:=\:\frac{\pi}{\mathrm{3}} \\ $$$$\underset{\:\sqrt{\mathrm{2}}} {\overset{\mathrm{2}} {\int}}\frac{\mathrm{sec}^{\mathrm{2}} \left(\mathrm{sec}^{−\mathrm{1}} \mathrm{x}\right)}{\mathrm{x}\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}}{dx}\:=\:\underset{\frac{\pi}{\mathrm{4}}} {\overset{\frac{\pi}{\mathrm{3}}} {\int}}{sec}^{\mathrm{2}} \left({y}\right)\centerdot{dy} \\ $$$$=\:\left[{tan}\left({y}\right)\right]_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{3}}} \\ $$$$=\:{tan}\left(\frac{\pi}{\mathrm{3}}\right)\:−\:{tan}\left(\frac{\pi}{\mathrm{4}}\right)\:=\:\sqrt{\mathrm{3}}\:−\:\mathrm{1} \\ $$$$ \\ $$$$ \\ $$
