Question Number 166431 by BagusSetyoWibowo last updated on 20/Feb/22
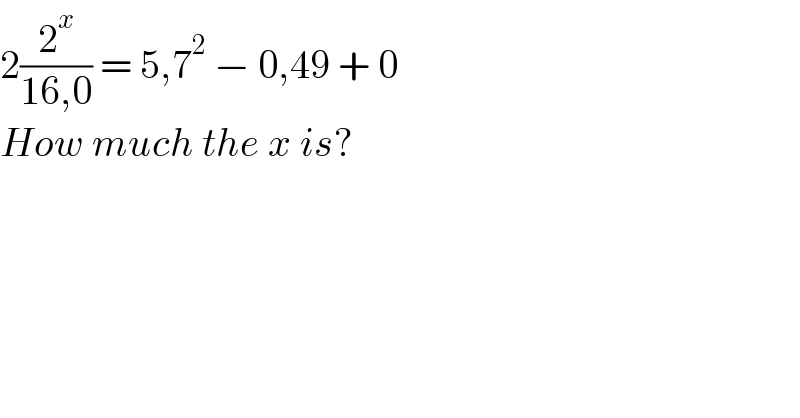
$$\mathrm{2}\frac{\mathrm{2}^{{x}} }{\mathrm{16},\mathrm{0}}\:=\:\mathrm{5},\mathrm{7}^{\mathrm{2}} \:−\:\mathrm{0},\mathrm{49}\:+\:\mathrm{0} \\ $$$${How}\:{much}\:{the}\:{x}\:{is}? \\ $$
Answered by alephzero last updated on 20/Feb/22
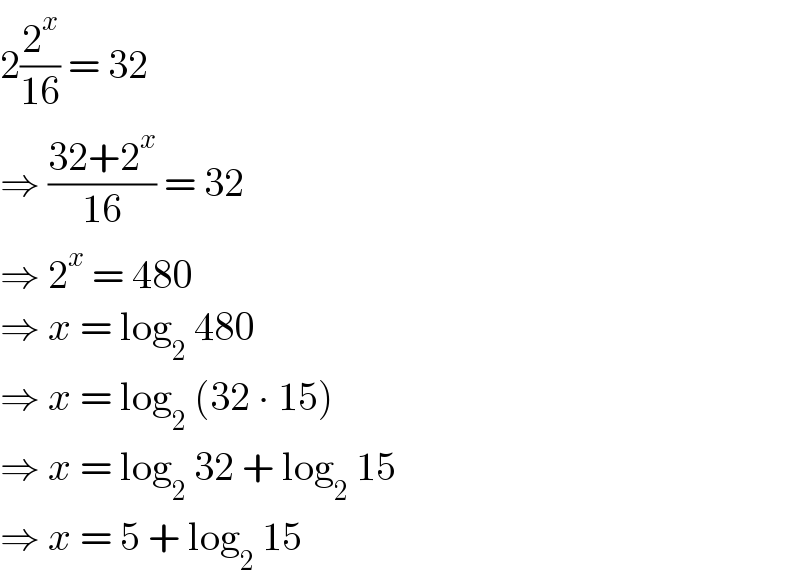
$$\mathrm{2}\frac{\mathrm{2}^{{x}} }{\mathrm{16}}\:=\:\mathrm{32} \\ $$$$\Rightarrow\:\frac{\mathrm{32}+\mathrm{2}^{{x}} }{\mathrm{16}}\:=\:\mathrm{32} \\ $$$$\Rightarrow\:\mathrm{2}^{{x}} \:=\:\mathrm{480} \\ $$$$\Rightarrow\:{x}\:=\:\mathrm{log}_{\mathrm{2}} \:\mathrm{480} \\ $$$$\Rightarrow\:{x}\:=\:\mathrm{log}_{\mathrm{2}} \:\left(\mathrm{32}\:\centerdot\:\mathrm{15}\right) \\ $$$$\Rightarrow\:{x}\:=\:\mathrm{log}_{\mathrm{2}} \:\mathrm{32}\:+\:\mathrm{log}_{\mathrm{2}} \:\mathrm{15} \\ $$$$\Rightarrow\:{x}\:=\:\mathrm{5}\:+\:\mathrm{log}_{\mathrm{2}} \:\mathrm{15} \\ $$
