Question Number 124446 by ZiYangLee last updated on 03/Dec/20
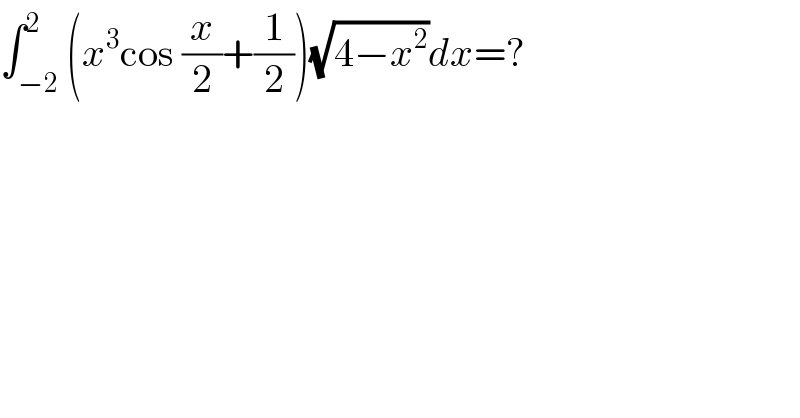
$$\int_{−\mathrm{2}} ^{\mathrm{2}} \left({x}^{\mathrm{3}} \mathrm{cos}\:\frac{{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\right)\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }{dx}=? \\ $$
Answered by Ar Brandon last updated on 03/Dec/20
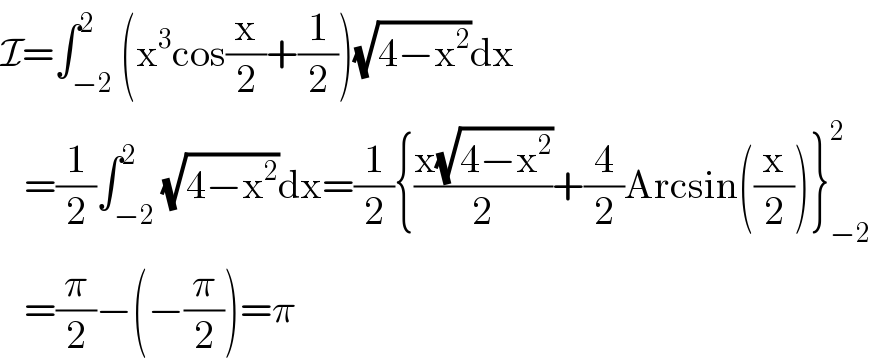
$$\mathcal{I}=\int_{−\mathrm{2}} ^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{3}} \mathrm{cos}\frac{\mathrm{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\right)\sqrt{\mathrm{4}−\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{−\mathrm{2}} ^{\mathrm{2}} \sqrt{\mathrm{4}−\mathrm{x}^{\mathrm{2}} }\mathrm{dx}=\frac{\mathrm{1}}{\mathrm{2}}\left\{\frac{\mathrm{x}\sqrt{\mathrm{4}−\mathrm{x}^{\mathrm{2}} }}{\mathrm{2}}+\frac{\mathrm{4}}{\mathrm{2}}\mathrm{Arcsin}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\right\}_{−\mathrm{2}} ^{\mathrm{2}} \\ $$$$\:\:\:=\frac{\pi}{\mathrm{2}}−\left(−\frac{\pi}{\mathrm{2}}\right)=\pi \\ $$
Commented by Ar Brandon last updated on 03/Dec/20
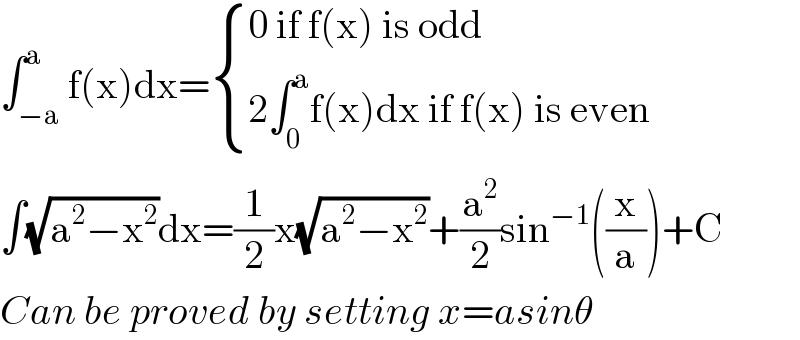
$$\int_{−\mathrm{a}} ^{\mathrm{a}} \mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=\begin{cases}{\mathrm{0}\:\mathrm{if}\:\mathrm{f}\left(\mathrm{x}\right)\:\mathrm{is}\:\mathrm{odd}}\\{\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{a}} \mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}\:\mathrm{if}\:\mathrm{f}\left(\mathrm{x}\right)\:\mathrm{is}\:\mathrm{even}}\end{cases} \\ $$$$\int\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{x}^{\mathrm{2}} }\mathrm{dx}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{x}^{\mathrm{2}} }+\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{2}}\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{x}}{\mathrm{a}}\right)+\mathrm{C} \\ $$$${Can}\:{be}\:{proved}\:{by}\:{setting}\:{x}={asin}\theta \\ $$
Answered by Dwaipayan Shikari last updated on 03/Dec/20
![∫_(−2) ^2 (x^3 cos(x/2)+(1/2))(√(4−x^2 )) dx =∫_(−2) ^2 (−x^3 cos(x/2)+(1/2))(√(4−x^2 )) dx=I 2I=∫_(−2) ^2 (√(4−x^2 )) dx 2I=∫_(−2) ^2 (√(4−x^2 )) dx =∫_(−1) ^1 (√(4−4sin^2 θ)) dθ x=2sinθ⇒1=2cosθ(dθ/dx) =2∫_0 ^(π/2) 1+cos2θ= π+2∫_0 ^(π/2) cos2θ =π+(1/2)[sin2θ]_0 ^(π/2) =π](https://www.tinkutara.com/question/Q124450.png)
$$\int_{−\mathrm{2}} ^{\mathrm{2}} \left({x}^{\mathrm{3}} {cos}\frac{{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\right)\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }\:{dx}\:\:=\int_{−\mathrm{2}} ^{\mathrm{2}} \left(−{x}^{\mathrm{3}} {cos}\frac{{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\right)\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }\:{dx}={I} \\ $$$$\mathrm{2}{I}=\int_{−\mathrm{2}} ^{\mathrm{2}} \sqrt{\mathrm{4}−{x}^{\mathrm{2}} }\:{dx} \\ $$$$\mathrm{2}{I}=\int_{−\mathrm{2}} ^{\mathrm{2}} \sqrt{\mathrm{4}−{x}^{\mathrm{2}} }\:{dx}\:=\int_{−\mathrm{1}} ^{\mathrm{1}} \sqrt{\mathrm{4}−\mathrm{4}{sin}^{\mathrm{2}} \theta}\:\:{d}\theta\:\:\:\:\:{x}=\mathrm{2}{sin}\theta\Rightarrow\mathrm{1}=\mathrm{2}{cos}\theta\frac{{d}\theta}{{dx}} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{1}+{cos}\mathrm{2}\theta=\:\pi+\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cos}\mathrm{2}\theta\:=\pi+\frac{\mathrm{1}}{\mathrm{2}}\left[{sin}\mathrm{2}\theta\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} =\pi \\ $$
Commented by Dwaipayan Shikari last updated on 03/Dec/20
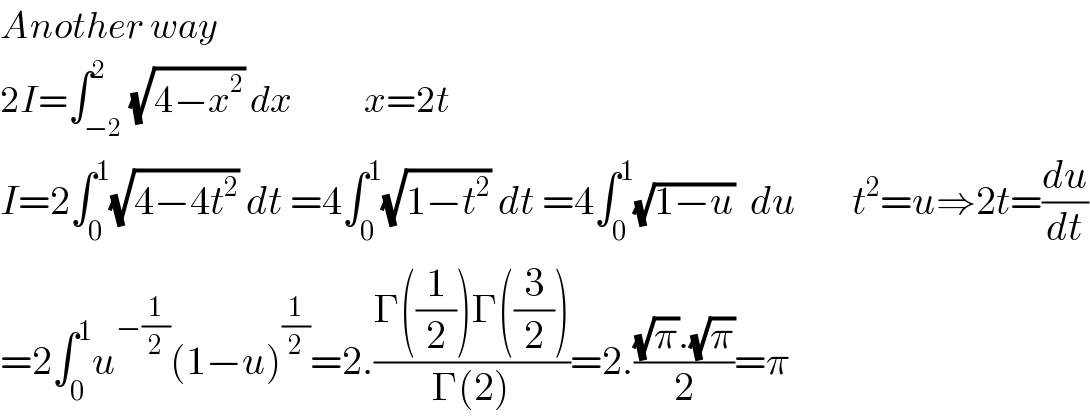
$${Another}\:{way} \\ $$$$\mathrm{2}{I}=\int_{−\mathrm{2}} ^{\mathrm{2}} \sqrt{\mathrm{4}−{x}^{\mathrm{2}} }\:{dx}\:\:\:\:\:\:\:\:\:\:\:\:{x}=\mathrm{2}{t} \\ $$$${I}=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{4}−\mathrm{4}{t}^{\mathrm{2}} }\:{dt}\:=\mathrm{4}\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{1}−{t}^{\mathrm{2}} }\:{dt}\:=\mathrm{4}\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{1}−{u}}\:\:{du}\:\:\:\:\:\:\:{t}^{\mathrm{2}} ={u}\Rightarrow\mathrm{2}{t}=\frac{{du}}{{dt}} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} {u}^{−\frac{\mathrm{1}}{\mathrm{2}}} \left(\mathrm{1}−{u}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} =\mathrm{2}.\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)}{\Gamma\left(\mathrm{2}\right)}=\mathrm{2}.\frac{\sqrt{\pi}.\sqrt{\pi}}{\mathrm{2}}=\pi \\ $$
