Question Number 160969 by mkam last updated on 10/Dec/21
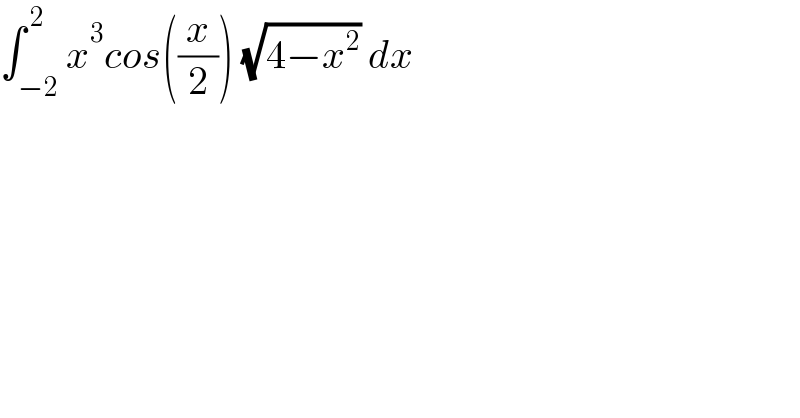
$$\int_{−\mathrm{2}} ^{\:\mathrm{2}} {x}^{\mathrm{3}} {cos}\left(\frac{{x}}{\mathrm{2}}\right)\:\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }\:{dx} \\ $$
Answered by MJS_new last updated on 10/Dec/21
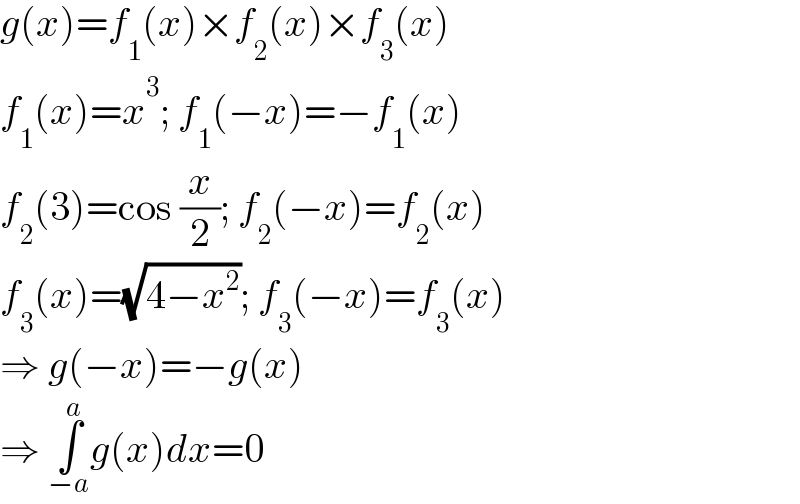
$${g}\left({x}\right)={f}_{\mathrm{1}} \left({x}\right)×{f}_{\mathrm{2}} \left({x}\right)×{f}_{\mathrm{3}} \left({x}\right) \\ $$$${f}_{\mathrm{1}} \left({x}\right)={x}^{\mathrm{3}} ;\:{f}_{\mathrm{1}} \left(−{x}\right)=−{f}_{\mathrm{1}} \left({x}\right) \\ $$$${f}_{\mathrm{2}} \left(\mathrm{3}\right)=\mathrm{cos}\:\frac{{x}}{\mathrm{2}};\:{f}_{\mathrm{2}} \left(−{x}\right)={f}_{\mathrm{2}} \left({x}\right) \\ $$$${f}_{\mathrm{3}} \left({x}\right)=\sqrt{\mathrm{4}−{x}^{\mathrm{2}} };\:{f}_{\mathrm{3}} \left(−{x}\right)={f}_{\mathrm{3}} \left({x}\right) \\ $$$$\Rightarrow\:{g}\left(−{x}\right)=−{g}\left({x}\right) \\ $$$$\Rightarrow\:\underset{−{a}} {\overset{{a}} {\int}}{g}\left({x}\right){dx}=\mathrm{0} \\ $$
