Question Number 175849 by Linton last updated on 08/Sep/22

$$\mathrm{2}^{\mathrm{2}{a}} +\mathrm{2}^{{a}} =\:\mathrm{10} \\ $$$${what}\:{is}\:{a}? \\ $$
Answered by MJS_new last updated on 08/Sep/22

$$\mathrm{2}^{\mathrm{2}{a}} +\mathrm{2}^{{a}} −\mathrm{10}=\mathrm{0} \\ $$$$\left(\mathrm{2}^{{a}} \right)^{\mathrm{2}} +\mathrm{2}^{{a}} −\mathrm{10}=\mathrm{0} \\ $$$$\mathrm{2}^{{a}} =−\frac{\mathrm{1}}{\mathrm{2}}\pm\sqrt{\frac{\mathrm{1}}{\mathrm{4}}+\mathrm{10}}=−\frac{\mathrm{1}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{41}}}{\mathrm{2}} \\ $$$$\mathrm{2}^{{a}} >\mathrm{0}\forall{a}\in\mathbb{R}\:\Rightarrow\:\mathrm{2}^{{a}} =\frac{−\mathrm{1}+\sqrt{\mathrm{41}}}{\mathrm{2}} \\ $$$${a}=\frac{\mathrm{ln}\:\frac{−\mathrm{1}+\sqrt{\mathrm{41}}}{\mathrm{2}}}{\mathrm{ln}\:\mathrm{2}}=\frac{\mathrm{ln}\:\left(−\mathrm{1}+\sqrt{\mathrm{41}}\right)}{\mathrm{ln}\:\mathrm{2}}−\mathrm{1} \\ $$
Answered by BaliramKumar last updated on 08/Sep/22
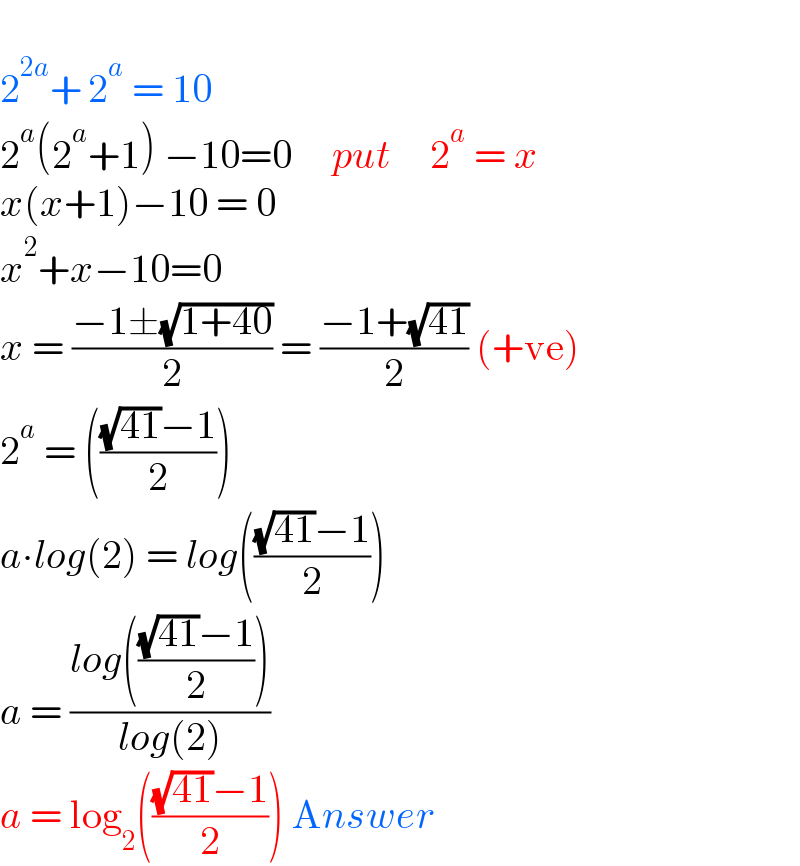
$$ \\ $$$$\mathrm{2}^{\mathrm{2}{a}} +\:\mathrm{2}^{{a}} \:=\:\mathrm{10} \\ $$$$\mathrm{2}^{{a}} \left(\mathrm{2}^{{a}} +\mathrm{1}\right)\:−\mathrm{10}=\mathrm{0}\:\:\:\:\:{put}\:\:\:\:\:\mathrm{2}^{{a}} \:=\:{x} \\ $$$${x}\left({x}+\mathrm{1}\right)−\mathrm{10}\:=\:\mathrm{0} \\ $$$${x}^{\mathrm{2}} +{x}−\mathrm{10}=\mathrm{0} \\ $$$${x}\:=\:\frac{−\mathrm{1}\pm\sqrt{\mathrm{1}+\mathrm{40}}}{\mathrm{2}}\:=\:\frac{−\mathrm{1}+\sqrt{\mathrm{41}}}{\mathrm{2}}\:\left(+\mathrm{ve}\right) \\ $$$$\mathrm{2}^{{a}} \:=\:\left(\frac{\sqrt{\mathrm{41}}−\mathrm{1}}{\mathrm{2}}\right) \\ $$$${a}\centerdot{log}\left(\mathrm{2}\right)\:=\:{log}\left(\frac{\sqrt{\mathrm{41}}−\mathrm{1}}{\mathrm{2}}\right) \\ $$$${a}\:=\:\frac{{log}\left(\frac{\sqrt{\mathrm{41}}−\mathrm{1}}{\mathrm{2}}\right)}{{log}\left(\mathrm{2}\right)} \\ $$$${a}\:=\:\mathrm{log}_{\mathrm{2}} \left(\frac{\sqrt{\mathrm{41}}−\mathrm{1}}{\mathrm{2}}\right)\:\mathrm{A}{nswer} \\ $$
