Menu Close

2-2e-2-ln-e-x-e-x-9-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 126316 by benjo_mathlover last updated on 19/Dec/20
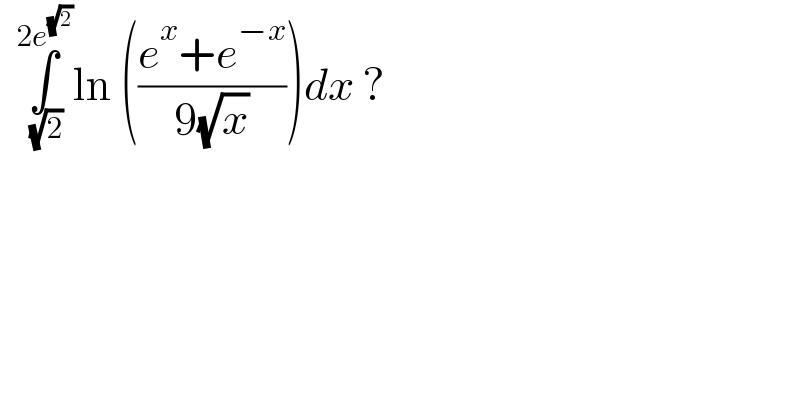
∫_( (√2)) ^(2e^(√2) ) ln (((e^x +e^(−x) )/(9(√x))))dx ?
$$\:\:\underset{\:\sqrt{\mathrm{2}}} {\overset{\mathrm{2}{e}^{\sqrt{\mathrm{2}}} } {\int}}\mathrm{ln}\:\left(\frac{{e}^{{x}} +{e}^{−{x}} }{\mathrm{9}\sqrt{{x}}}\right){dx}\:?\: \\ $$
Commented by liberty last updated on 19/Dec/20
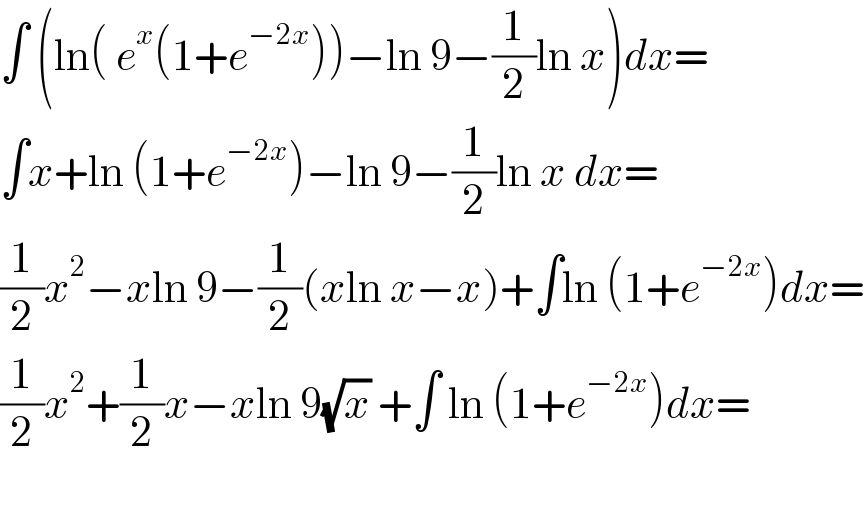
∫ (ln( e^x (1+e^(−2x) ))−ln 9−(1/2)ln x)dx= ∫x+ln (1+e^(−2x) )−ln 9−(1/2)ln x dx= (1/2)x^2 −xln 9−(1/2)(xln x−x)+∫ln (1+e^(−2x) )dx= (1/2)x^2 +(1/2)x−xln 9(√x) +∫ ln (1+e^(−2x) )dx=
$$\int\:\left(\mathrm{ln}\left(\:{e}^{{x}} \left(\mathrm{1}+{e}^{−\mathrm{2}{x}} \right)\right)−\mathrm{ln}\:\mathrm{9}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:{x}\right){dx}= \\ $$$$\int{x}+\mathrm{ln}\:\left(\mathrm{1}+{e}^{−\mathrm{2}{x}} \right)−\mathrm{ln}\:\mathrm{9}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:{x}\:{dx}= \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} −{x}\mathrm{ln}\:\mathrm{9}−\frac{\mathrm{1}}{\mathrm{2}}\left({x}\mathrm{ln}\:{x}−{x}\right)+\int\mathrm{ln}\:\left(\mathrm{1}+{e}^{−\mathrm{2}{x}} \right){dx}= \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}{x}−{x}\mathrm{ln}\:\mathrm{9}\sqrt{{x}}\:+\int\:\mathrm{ln}\:\left(\mathrm{1}+{e}^{−\mathrm{2}{x}} \right){dx}= \\ $$$$ \\ $$
Commented by Olaf last updated on 19/Dec/20
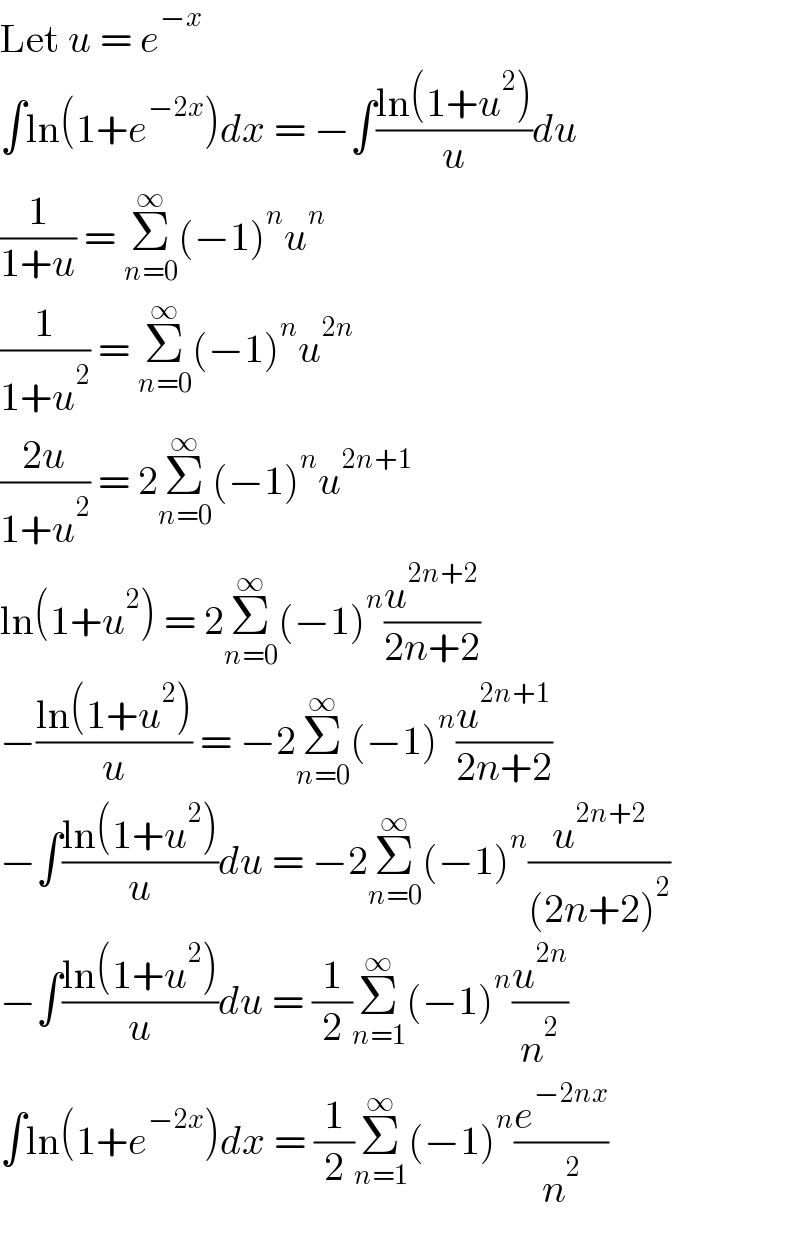
Let u = e^(−x) ∫ln(1+e^(−2x) )dx = −∫((ln(1+u^2 ))/u)du (1/(1+u)) = Σ_(n=0) ^∞ (−1)^n u^n (1/(1+u^2 )) = Σ_(n=0) ^∞ (−1)^n u^(2n) ((2u)/(1+u^2 )) = 2Σ_(n=0) ^∞ (−1)^n u^(2n+1) ln(1+u^2 ) = 2Σ_(n=0) ^∞ (−1)^n (u^(2n+2) /(2n+2)) −((ln(1+u^2 ))/u) = −2Σ_(n=0) ^∞ (−1)^n (u^(2n+1) /(2n+2)) −∫((ln(1+u^2 ))/u)du = −2Σ_(n=0) ^∞ (−1)^n (u^(2n+2) /((2n+2)^2 )) −∫((ln(1+u^2 ))/u)du = (1/2)Σ_(n=1) ^∞ (−1)^n (u^(2n) /n^2 ) ∫ln(1+e^(−2x) )dx = (1/2)Σ_(n=1) ^∞ (−1)^n (e^(−2nx) /n^2 )
$$\mathrm{Let}\:{u}\:=\:{e}^{−{x}} \\ $$$$\int\mathrm{ln}\left(\mathrm{1}+{e}^{−\mathrm{2}{x}} \right){dx}\:=\:−\int\frac{\mathrm{ln}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)}{{u}}{du} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}+{u}}\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} {u}^{{n}} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}+{u}^{\mathrm{2}} }\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} {u}^{\mathrm{2}{n}} \\ $$$$\frac{\mathrm{2}{u}}{\mathrm{1}+{u}^{\mathrm{2}} }\:=\:\mathrm{2}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} {u}^{\mathrm{2}{n}+\mathrm{1}} \\ $$$$\mathrm{ln}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)\:=\:\mathrm{2}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \frac{{u}^{\mathrm{2}{n}+\mathrm{2}} }{\mathrm{2}{n}+\mathrm{2}} \\ $$$$−\frac{\mathrm{ln}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)}{{u}}\:=\:−\mathrm{2}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \frac{{u}^{\mathrm{2}{n}+\mathrm{1}} }{\mathrm{2}{n}+\mathrm{2}} \\ $$$$−\int\frac{\mathrm{ln}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)}{{u}}{du}\:=\:−\mathrm{2}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \frac{{u}^{\mathrm{2}{n}+\mathrm{2}} }{\left(\mathrm{2}{n}+\mathrm{2}\right)^{\mathrm{2}} } \\ $$$$−\int\frac{\mathrm{ln}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)}{{u}}{du}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \frac{{u}^{\mathrm{2}{n}} }{{n}^{\mathrm{2}} } \\ $$$$\int\mathrm{ln}\left(\mathrm{1}+{e}^{−\mathrm{2}{x}} \right){dx}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \frac{{e}^{−\mathrm{2}{nx}} }{{n}^{\mathrm{2}} } \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *