Question Number 124452 by liberty last updated on 03/Dec/20
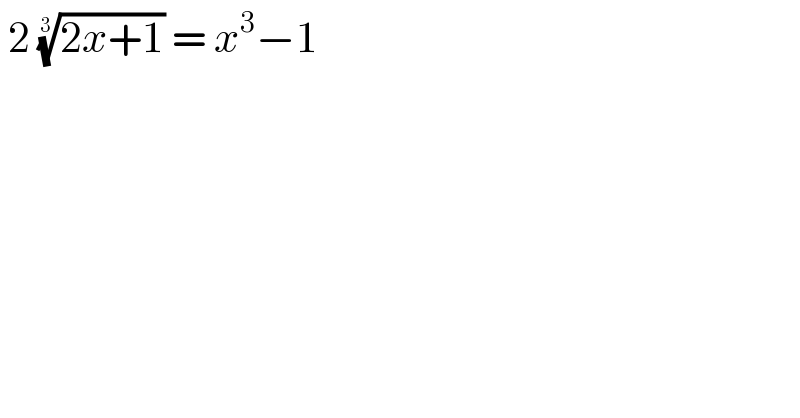
$$\:\mathrm{2}\:\sqrt[{\mathrm{3}}]{\mathrm{2}{x}+\mathrm{1}}\:=\:{x}^{\mathrm{3}} −\mathrm{1}\: \\ $$
Commented by Dwaipayan Shikari last updated on 03/Dec/20
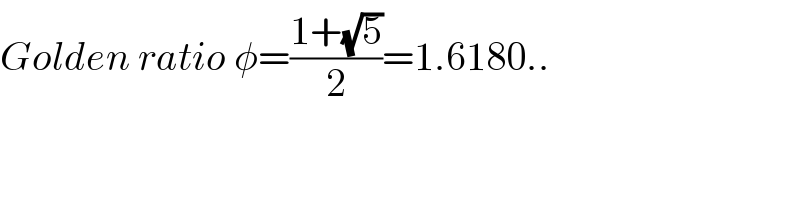
$${Golden}\:{ratio}\:\phi=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}=\mathrm{1}.\mathrm{6180}.. \\ $$
Answered by mnjuly1970 last updated on 03/Dec/20
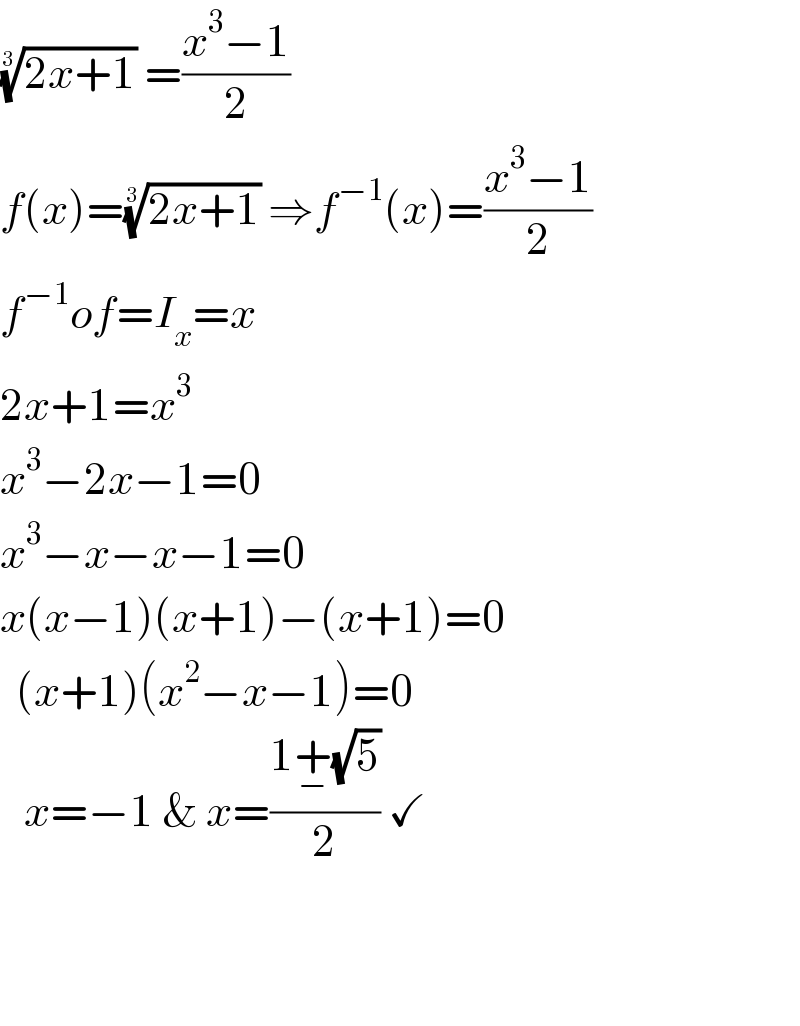
$$\sqrt[{\mathrm{3}}]{\mathrm{2}{x}+\mathrm{1}}\:=\frac{{x}^{\mathrm{3}} −\mathrm{1}}{\mathrm{2}} \\ $$$${f}\left({x}\right)=\sqrt[{\mathrm{3}}]{\mathrm{2}{x}+\mathrm{1}}\:\Rightarrow{f}^{−\mathrm{1}} \left({x}\right)=\frac{{x}^{\mathrm{3}} −\mathrm{1}}{\mathrm{2}} \\ $$$${f}^{−\mathrm{1}} {of}={I}_{{x}} ={x} \\ $$$$\mathrm{2}{x}+\mathrm{1}={x}^{\mathrm{3}} \\ $$$${x}^{\mathrm{3}} −\mathrm{2}{x}−\mathrm{1}=\mathrm{0} \\ $$$${x}^{\mathrm{3}} −{x}−{x}−\mathrm{1}=\mathrm{0} \\ $$$${x}\left({x}−\mathrm{1}\right)\left({x}+\mathrm{1}\right)−\left({x}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\:\:\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −{x}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\:\:\:{x}=−\mathrm{1}\:\&\:{x}=\frac{\mathrm{1}\underset{−} {+}\sqrt{\mathrm{5}}}{\mathrm{2}}\:\checkmark \\ $$$$ \\ $$$$\:\: \\ $$
Commented by MJS_new last updated on 03/Dec/20
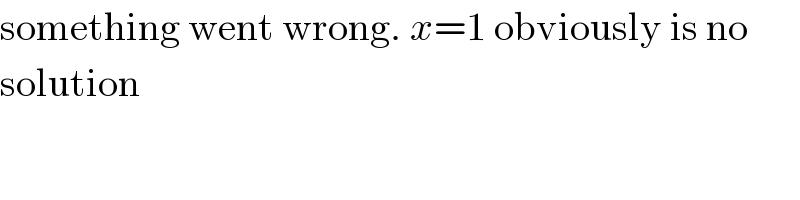
$$\mathrm{something}\:\mathrm{went}\:\mathrm{wrong}.\:{x}=\mathrm{1}\:\mathrm{obviously}\:\mathrm{is}\:\mathrm{no} \\ $$$$\mathrm{solution} \\ $$
Commented by mnjuly1970 last updated on 03/Dec/20
$${thank}\:{you}\:{mr}\:{mjs}.. \\ $$$${you}\:{are}\:{right}.. \\ $$$${i}\:{made}\:\:{a}\:{mistake}\:{in}\:{the} \\ $$$${calulation}\:\left({decomposition}\:\right) \\ $$
Commented by mnjuly1970 last updated on 03/Dec/20

$$ \\ $$
