Menu Close

2-2x-1-1-3-x-3-1-How-much-the-x-is-

Tinku Tara 0 Comments
Pin




Question Number 167508 by Bagus1003 last updated on 18/Mar/22
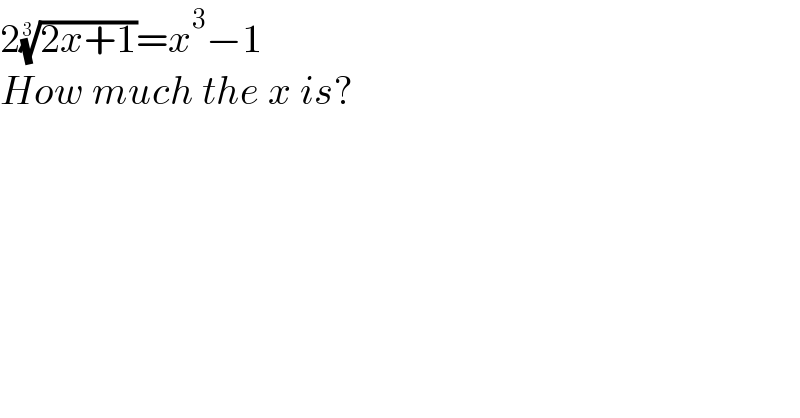
2((2x+1))^(1/3) =x^3 −1 How much the x is?
$$\mathrm{2}\sqrt[{\mathrm{3}}]{\mathrm{2}{x}+\mathrm{1}}={x}^{\mathrm{3}} −\mathrm{1} \\ $$$${How}\:{much}\:{the}\:{x}\:{is}? \\ $$
Answered by alephzero last updated on 18/Mar/22
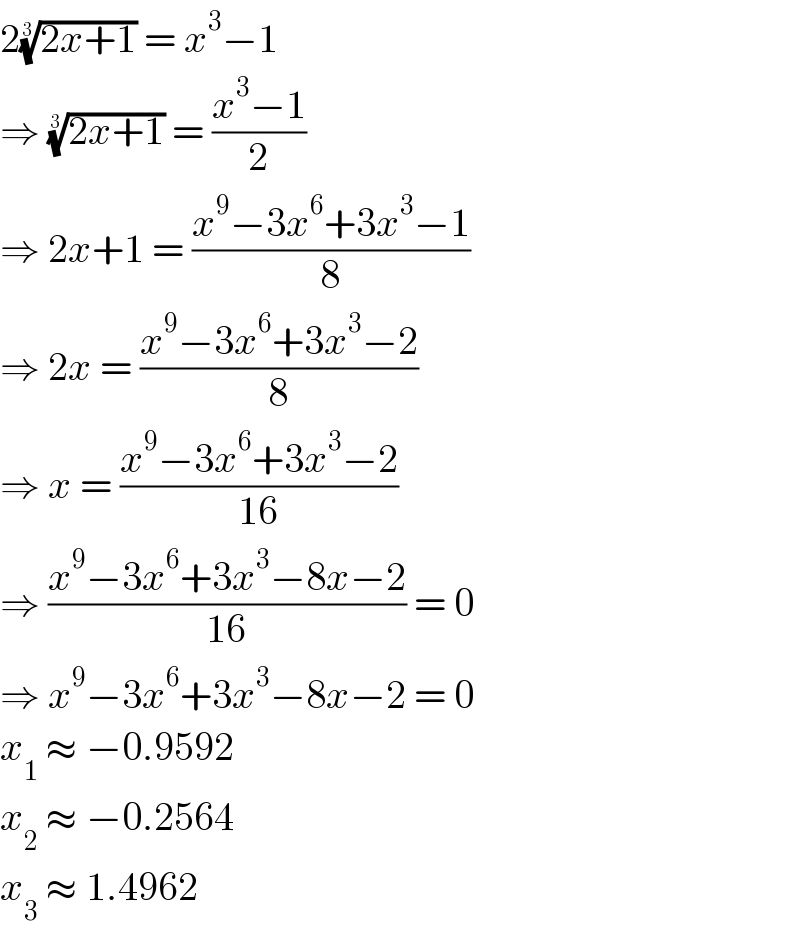
2((2x+1))^(1/3) = x^3 −1 ⇒ ((2x+1))^(1/3) = ((x^3 −1)/2) ⇒ 2x+1 = ((x^9 −3x^6 +3x^3 −1)/8) ⇒ 2x = ((x^9 −3x^6 +3x^3 −2)/8) ⇒ x = ((x^9 −3x^6 +3x^3 −2)/(16)) ⇒ ((x^9 −3x^6 +3x^3 −8x−2)/(16)) = 0 ⇒ x^9 −3x^6 +3x^3 −8x−2 = 0 x_1 ≈ −0.9592 x_2 ≈ −0.2564 x_3 ≈ 1.4962
$$\mathrm{2}\sqrt[{\mathrm{3}}]{\mathrm{2}{x}+\mathrm{1}}\:=\:{x}^{\mathrm{3}} −\mathrm{1} \\ $$$$\Rightarrow\:\sqrt[{\mathrm{3}}]{\mathrm{2}{x}+\mathrm{1}}\:=\:\frac{{x}^{\mathrm{3}} −\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{2}{x}+\mathrm{1}\:=\:\frac{{x}^{\mathrm{9}} −\mathrm{3}{x}^{\mathrm{6}} +\mathrm{3}{x}^{\mathrm{3}} −\mathrm{1}}{\mathrm{8}} \\ $$$$\Rightarrow\:\mathrm{2}{x}\:=\:\frac{{x}^{\mathrm{9}} −\mathrm{3}{x}^{\mathrm{6}} +\mathrm{3}{x}^{\mathrm{3}} −\mathrm{2}}{\mathrm{8}} \\ $$$$\Rightarrow\:{x}\:=\:\frac{{x}^{\mathrm{9}} −\mathrm{3}{x}^{\mathrm{6}} +\mathrm{3}{x}^{\mathrm{3}} −\mathrm{2}}{\mathrm{16}} \\ $$$$\Rightarrow\:\frac{{x}^{\mathrm{9}} −\mathrm{3}{x}^{\mathrm{6}} +\mathrm{3}{x}^{\mathrm{3}} −\mathrm{8}{x}−\mathrm{2}}{\mathrm{16}}\:=\:\mathrm{0} \\ $$$$\Rightarrow\:{x}^{\mathrm{9}} −\mathrm{3}{x}^{\mathrm{6}} +\mathrm{3}{x}^{\mathrm{3}} −\mathrm{8}{x}−\mathrm{2}\:=\:\mathrm{0} \\ $$$${x}_{\mathrm{1}} \:\approx\:−\mathrm{0}.\mathrm{9592} \\ $$$${x}_{\mathrm{2}} \:\approx\:−\mathrm{0}.\mathrm{2564} \\ $$$${x}_{\mathrm{3}} \:\approx\:\mathrm{1}.\mathrm{4962} \\ $$
Answered by Jamshidbek last updated on 18/Mar/22
Solution. 2x+1=t ⇒ 2x=t−1 2((2x+1))^(1/3) =x^3 −1 ⇒ 16((2x+1))^(1/3) =(2x)^3 −8 ⇒ 16t=(t−1)^3 −8 ⇒ t^3 −3t^2 +3t−1−8=16t t^3 −3t^2 −13t−9=0 t^3 +t^2 −4t^2 −4t−9t−9=0 t^2 (t+1)−4t(t+1)−9(t+1)=0 (t+1)(t^2 −4t−9)=0 t_1 =−1 t_(2,3) =((4±(√(52)))/2)=2±(√(13)) x_1 =−1 x_(2,3) =((2±(√(13))−1)/2)=((1±(√(13)))/2) Telegram:@math_undergraduate
$$\mathrm{Solution}. \\ $$$$\mathrm{2x}+\mathrm{1}=\mathrm{t}\:\Rightarrow\:\mathrm{2x}=\mathrm{t}−\mathrm{1} \\ $$$$\mathrm{2}\sqrt[{\mathrm{3}}]{\mathrm{2x}+\mathrm{1}}=\mathrm{x}^{\mathrm{3}} −\mathrm{1}\:\Rightarrow\:\mathrm{16}\sqrt[{\mathrm{3}}]{\mathrm{2x}+\mathrm{1}}=\left(\mathrm{2x}\right)^{\mathrm{3}} −\mathrm{8}\:\Rightarrow \\ $$$$\mathrm{16t}=\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{3}} −\mathrm{8}\:\Rightarrow\:\mathrm{t}^{\mathrm{3}} −\mathrm{3t}^{\mathrm{2}} +\mathrm{3t}−\mathrm{1}−\mathrm{8}=\mathrm{16t} \\ $$$$\mathrm{t}^{\mathrm{3}} −\mathrm{3t}^{\mathrm{2}} −\mathrm{13t}−\mathrm{9}=\mathrm{0} \\ $$$$\mathrm{t}^{\mathrm{3}} +\mathrm{t}^{\mathrm{2}} −\mathrm{4t}^{\mathrm{2}} −\mathrm{4t}−\mathrm{9t}−\mathrm{9}=\mathrm{0} \\ $$$$\mathrm{t}^{\mathrm{2}} \left(\mathrm{t}+\mathrm{1}\right)−\mathrm{4t}\left(\mathrm{t}+\mathrm{1}\right)−\mathrm{9}\left(\mathrm{t}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\left(\mathrm{t}+\mathrm{1}\right)\left(\mathrm{t}^{\mathrm{2}} −\mathrm{4t}−\mathrm{9}\right)=\mathrm{0} \\ $$$$\mathrm{t}_{\mathrm{1}} =−\mathrm{1}\:\:\mathrm{t}_{\mathrm{2},\mathrm{3}} =\frac{\mathrm{4}\pm\sqrt{\mathrm{52}}}{\mathrm{2}}=\mathrm{2}\pm\sqrt{\mathrm{13}} \\ $$$$\mathrm{x}_{\mathrm{1}} =−\mathrm{1}\:\:\mathrm{x}_{\mathrm{2},\mathrm{3}} =\frac{\mathrm{2}\pm\sqrt{\mathrm{13}}−\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{1}\pm\sqrt{\mathrm{13}}}{\mathrm{2}} \\ $$$$\mathrm{Telegram}:@\mathrm{math\_undergraduate} \\ $$
Commented by mr W last updated on 18/Mar/22
x_1 =−1 x_(2,3) =((1±(√5))/2)
$$\mathrm{x}_{\mathrm{1}} =−\mathrm{1}\:\:\mathrm{x}_{\mathrm{2},\mathrm{3}} =\frac{\mathrm{1}\pm\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *