2-2x-1-3-2-4x-1-3-4-x-5-2-x-1-3-2-x-2-2-x-8-x-pleas-solve-thes-

Question Number 129841 by Adel last updated on 20/Jan/21

$$\left\{_{\sqrt[{\mathrm{3}}]{\mathrm{2}^{\mathrm{2x}} }+\sqrt[{\mathrm{3}}]{\mathrm{2}^{\mathrm{4x}} }+\mathrm{4}^{\mathrm{x}} =\mathrm{5}} ^{\sqrt[{\mathrm{3}}]{\mathrm{2}^{\mathrm{x}} \:}−\mathrm{2}^{\mathrm{x}} =\mathrm{2}} \right\}\Rightarrow\mathrm{2}^{\mathrm{x}} −\mathrm{8}^{\mathrm{x}} =? \\ $$$$\mathrm{pleas}\:\mathrm{solve}\:\mathrm{thes} \\ $$

Commented by MJS_new last updated on 20/Jan/21

2^(x/3) −2^x =2 2^(2x/3) +2^(4x/3) +4^x =5 has no solution at all if it′s a system of equations two independent equations: (1) 2^(x/3) −2^x =2 t=2^(x/3) ⇔ x=((3ln t)/(ln 2))∧t>0 t^3 −t+2=0 t≈−1.52 ⇒ no real solution for x (2) 2^(2x/3) +2^(4x/3) +4^x =5 t=2^(x/3) ⇔ x=((3ln t)/(ln 2))∧t>0 t^6 +t^4 +t^2 −5=0 u=t^2 +(1/3) ⇔ t=(√(u−(1/3)))∧u≥(1/3) u^3 +(2/3)u−((142)/(27))=0 u≈1.61149641 ⇒ t≈1.13055874 ⇒ x≈.531107869 2^x −8^x ≈−1.57239847

$$\mathrm{2}^{{x}/\mathrm{3}} −\mathrm{2}^{{x}} =\mathrm{2} \\ $$$$\mathrm{2}^{\mathrm{2}{x}/\mathrm{3}} +\mathrm{2}^{\mathrm{4}{x}/\mathrm{3}} +\mathrm{4}^{{x}} =\mathrm{5} \\ $$$$\mathrm{has}\:\mathrm{no}\:\mathrm{solution}\:\mathrm{at}\:\mathrm{all}\:\mathrm{if}\:\mathrm{it}'\mathrm{s}\:\mathrm{a}\:\mathrm{system}\:\mathrm{of}\:\mathrm{equations} \\ $$$$ \\ $$$$\mathrm{two}\:\mathrm{independent}\:\mathrm{equations}: \\ $$$$\left(\mathrm{1}\right) \\ $$$$\mathrm{2}^{{x}/\mathrm{3}} −\mathrm{2}^{{x}} =\mathrm{2} \\ $$$${t}=\mathrm{2}^{{x}/\mathrm{3}} \:\Leftrightarrow\:{x}=\frac{\mathrm{3ln}\:{t}}{\mathrm{ln}\:\mathrm{2}}\wedge{t}>\mathrm{0} \\ $$$${t}^{\mathrm{3}} −{t}+\mathrm{2}=\mathrm{0} \\ $$$${t}\approx−\mathrm{1}.\mathrm{52}\:\Rightarrow\:\mathrm{no}\:\mathrm{real}\:\mathrm{solution}\:\mathrm{for}\:{x} \\ $$$$\left(\mathrm{2}\right) \\ $$$$\mathrm{2}^{\mathrm{2}{x}/\mathrm{3}} +\mathrm{2}^{\mathrm{4}{x}/\mathrm{3}} +\mathrm{4}^{{x}} =\mathrm{5} \\ $$$${t}=\mathrm{2}^{{x}/\mathrm{3}} \:\Leftrightarrow\:{x}=\frac{\mathrm{3ln}\:{t}}{\mathrm{ln}\:\mathrm{2}}\wedge{t}>\mathrm{0} \\ $$$${t}^{\mathrm{6}} +{t}^{\mathrm{4}} +{t}^{\mathrm{2}} −\mathrm{5}=\mathrm{0} \\ $$$${u}={t}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{3}}\:\Leftrightarrow\:{t}=\sqrt{{u}−\frac{\mathrm{1}}{\mathrm{3}}}\wedge{u}\geqslant\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${u}^{\mathrm{3}} +\frac{\mathrm{2}}{\mathrm{3}}{u}−\frac{\mathrm{142}}{\mathrm{27}}=\mathrm{0} \\ $$$${u}\approx\mathrm{1}.\mathrm{61149641} \\ $$$$\Rightarrow\:{t}\approx\mathrm{1}.\mathrm{13055874} \\ $$$$\Rightarrow\:{x}\approx.\mathrm{531107869} \\ $$$$\mathrm{2}^{{x}} −\mathrm{8}^{{x}} \approx−\mathrm{1}.\mathrm{57239847} \\ $$

Commented by Adel last updated on 20/Jan/21

$$\mathrm{thanks} \\ $$

Answered by liberty last updated on 20/Jan/21

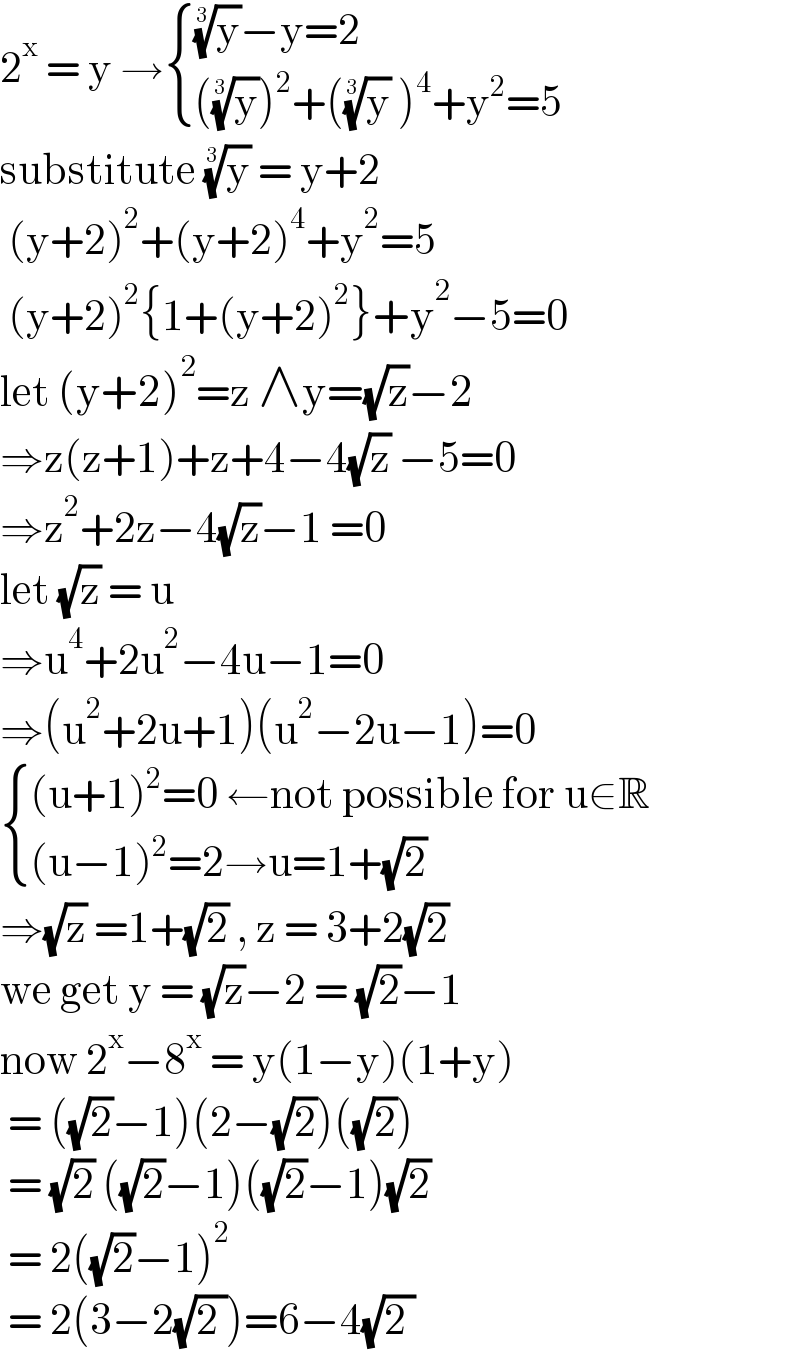
2^x = y → { (((y)^(1/3) −y=2)),((((y)^(1/3) )^2 +((y)^(1/3) )^4 +y^2 =5)) :} substitute (y)^(1/3) = y+2 (y+2)^2 +(y+2)^4 +y^2 =5 (y+2)^2 {1+(y+2)^2 }+y^2 −5=0 let (y+2)^2 =z ∧y=(√z)−2 ⇒z(z+1)+z+4−4(√z) −5=0 ⇒z^2 +2z−4(√z)−1 =0 let (√z) = u ⇒u^4 +2u^2 −4u−1=0 ⇒(u^2 +2u+1)(u^2 −2u−1)=0 { (((u+1)^2 =0 ←not possible for u∈R)),(((u−1)^2 =2→u=1+(√2))) :} ⇒(√z) =1+(√2) , z = 3+2(√2) we get y = (√z)−2 = (√2)−1 now 2^x −8^x = y(1−y)(1+y) = ((√2)−1)(2−(√2))((√2)) = (√2) ((√2)−1)((√2)−1)(√2) = 2((√2)−1)^2 = 2(3−2(√(2 )))=6−4(√(2 ))

$$\mathrm{2}^{\mathrm{x}} \:=\:\mathrm{y}\:\rightarrow\begin{cases}{\sqrt[{\mathrm{3}}]{\mathrm{y}}−\mathrm{y}=\mathrm{2}}\\{\left(\sqrt[{\mathrm{3}}]{\mathrm{y}}\right)^{\mathrm{2}} +\left(\sqrt[{\mathrm{3}}]{\mathrm{y}}\:\right)^{\mathrm{4}} +\mathrm{y}^{\mathrm{2}} =\mathrm{5}}\end{cases} \\ $$$$\mathrm{substitute}\:\sqrt[{\mathrm{3}}]{\mathrm{y}}\:=\:\mathrm{y}+\mathrm{2} \\ $$$$\:\left(\mathrm{y}+\mathrm{2}\right)^{\mathrm{2}} +\left(\mathrm{y}+\mathrm{2}\right)^{\mathrm{4}} +\mathrm{y}^{\mathrm{2}} =\mathrm{5}\: \\ $$$$\:\left(\mathrm{y}+\mathrm{2}\right)^{\mathrm{2}} \left\{\mathrm{1}+\left(\mathrm{y}+\mathrm{2}\right)^{\mathrm{2}} \right\}+\mathrm{y}^{\mathrm{2}} −\mathrm{5}=\mathrm{0} \\ $$$$\mathrm{let}\:\left(\mathrm{y}+\mathrm{2}\right)^{\mathrm{2}} =\mathrm{z}\:\wedge\mathrm{y}=\sqrt{\mathrm{z}}−\mathrm{2} \\ $$$$\Rightarrow\mathrm{z}\left(\mathrm{z}+\mathrm{1}\right)+\mathrm{z}+\mathrm{4}−\mathrm{4}\sqrt{\mathrm{z}}\:−\mathrm{5}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{z}^{\mathrm{2}} +\mathrm{2z}−\mathrm{4}\sqrt{\mathrm{z}}−\mathrm{1}\:=\mathrm{0} \\ $$$$\mathrm{let}\:\sqrt{\mathrm{z}}\:=\:\mathrm{u} \\ $$$$\Rightarrow\mathrm{u}^{\mathrm{4}} +\mathrm{2u}^{\mathrm{2}} −\mathrm{4u}−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{u}^{\mathrm{2}} +\mathrm{2u}+\mathrm{1}\right)\left(\mathrm{u}^{\mathrm{2}} −\mathrm{2u}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\begin{cases}{\left(\mathrm{u}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{0}\:\leftarrow\mathrm{not}\:\mathrm{possible}\:\mathrm{for}\:\mathrm{u}\in\mathbb{R}}\\{\left(\mathrm{u}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{2}\rightarrow\mathrm{u}=\mathrm{1}+\sqrt{\mathrm{2}}}\end{cases}\: \\ $$$$\Rightarrow\sqrt{\mathrm{z}}\:=\mathrm{1}+\sqrt{\mathrm{2}}\:,\:\mathrm{z}\:=\:\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}} \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{y}\:=\:\sqrt{\mathrm{z}}−\mathrm{2}\:=\:\sqrt{\mathrm{2}}−\mathrm{1} \\ $$$$\mathrm{now}\:\mathrm{2}^{\mathrm{x}} −\mathrm{8}^{\mathrm{x}} \:=\:\mathrm{y}\left(\mathrm{1}−\mathrm{y}\right)\left(\mathrm{1}+\mathrm{y}\right) \\ $$$$\:=\:\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\left(\mathrm{2}−\sqrt{\mathrm{2}}\right)\left(\sqrt{\mathrm{2}}\right) \\ $$$$\:=\:\sqrt{\mathrm{2}}\:\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\sqrt{\mathrm{2}} \\ $$$$\:=\:\mathrm{2}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\:=\:\mathrm{2}\left(\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}\:}\right)=\mathrm{6}−\mathrm{4}\sqrt{\mathrm{2}\:} \\ $$

Commented by Adel last updated on 20/Jan/21