Question Number 149171 by liberty last updated on 03/Aug/21
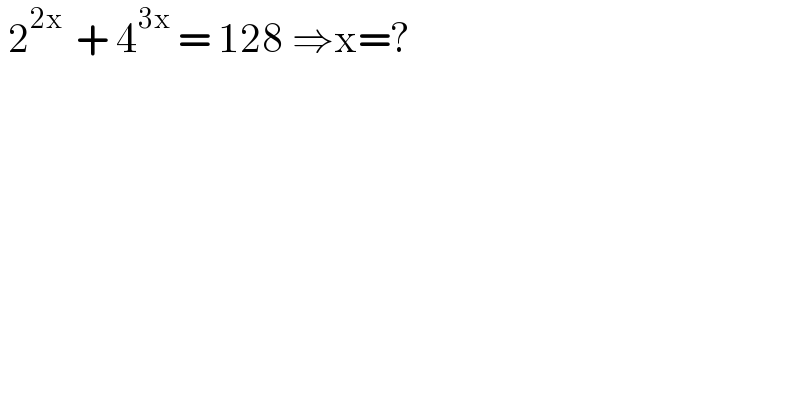
$$\:\mathrm{2}^{\mathrm{2x}\:} \:+\:\mathrm{4}^{\mathrm{3x}} \:=\:\mathrm{128}\:\Rightarrow\mathrm{x}=? \\ $$
Answered by Ar Brandon last updated on 03/Aug/21
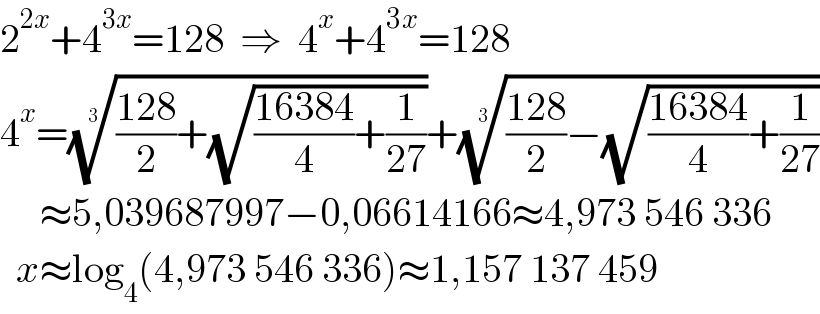
$$\mathrm{2}^{\mathrm{2}{x}} +\mathrm{4}^{\mathrm{3}{x}} =\mathrm{128}\:\:\Rightarrow\:\:\mathrm{4}^{{x}} +\mathrm{4}^{\mathrm{3}{x}} =\mathrm{128} \\ $$$$\mathrm{4}^{{x}} =\sqrt[{\mathrm{3}}]{\frac{\mathrm{128}}{\mathrm{2}}+\sqrt{\frac{\mathrm{16384}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{27}}}}+\sqrt[{\mathrm{3}}]{\frac{\mathrm{128}}{\mathrm{2}}−\sqrt{\frac{\mathrm{16384}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{27}}}} \\ $$$$\:\:\:\:\:\approx\mathrm{5},\mathrm{039687997}−\mathrm{0},\mathrm{06614166}\approx\mathrm{4},\mathrm{973}\:\mathrm{546}\:\mathrm{336} \\ $$$$\:\:{x}\approx\mathrm{log}_{\mathrm{4}} \left(\mathrm{4},\mathrm{973}\:\mathrm{546}\:\mathrm{336}\right)\approx\mathrm{1},\mathrm{157}\:\mathrm{137}\:\mathrm{459} \\ $$
Commented by liberty last updated on 03/Aug/21

$$\mathrm{Cardano} \\ $$
Answered by liberty last updated on 03/Aug/21

