Question Number 102783 by bramlex last updated on 11/Jul/20
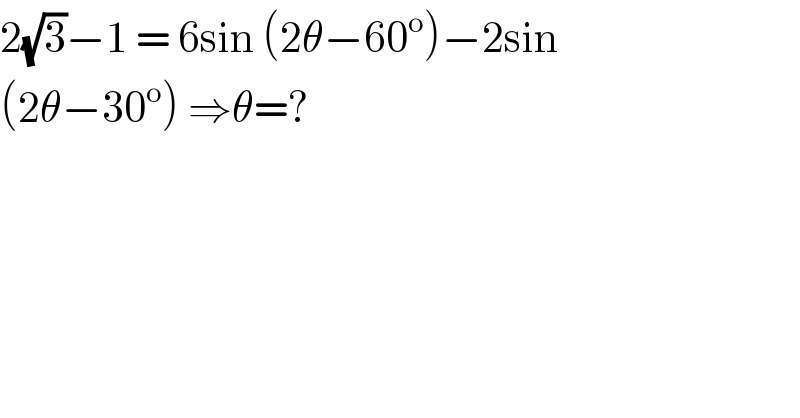
$$\mathrm{2}\sqrt{\mathrm{3}}−\mathrm{1}\:=\:\mathrm{6sin}\:\left(\mathrm{2}\theta−\mathrm{60}^{\mathrm{o}} \right)−\mathrm{2sin} \\ $$$$\left(\mathrm{2}\theta−\mathrm{30}^{\mathrm{o}} \right)\:\Rightarrow\theta=? \\ $$
Answered by 1549442205 last updated on 11/Jul/20
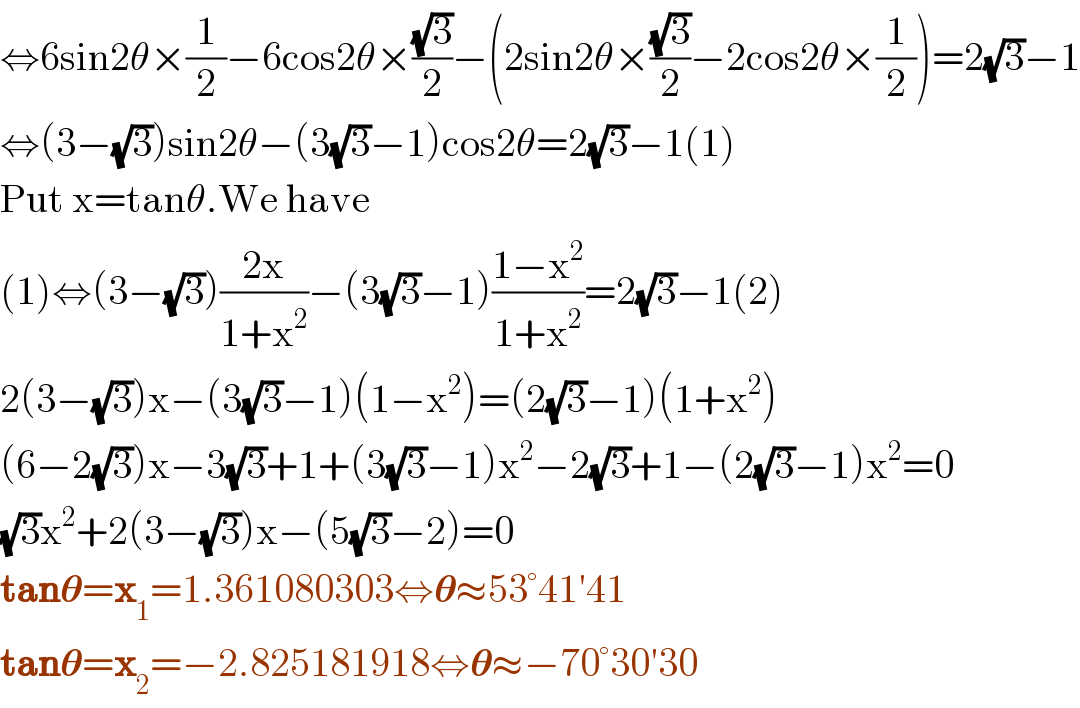
$$\Leftrightarrow\mathrm{6sin2}\theta×\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{6cos2}\theta×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\left(\mathrm{2sin2}\theta×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\mathrm{2cos2}\theta×\frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{2}\sqrt{\mathrm{3}}−\mathrm{1} \\ $$$$\Leftrightarrow\left(\mathrm{3}−\sqrt{\mathrm{3}}\right)\mathrm{sin2}\theta−\left(\mathrm{3}\sqrt{\mathrm{3}}−\mathrm{1}\right)\mathrm{cos2}\theta=\mathrm{2}\sqrt{\mathrm{3}}−\mathrm{1}\left(\mathrm{1}\right) \\ $$$$\mathrm{Put}\:\mathrm{x}=\mathrm{tan}\theta.\mathrm{We}\:\mathrm{have} \\ $$$$\left(\mathrm{1}\right)\Leftrightarrow\left(\mathrm{3}−\sqrt{\mathrm{3}}\right)\frac{\mathrm{2x}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }−\left(\mathrm{3}\sqrt{\mathrm{3}}−\mathrm{1}\right)\frac{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }=\mathrm{2}\sqrt{\mathrm{3}}−\mathrm{1}\left(\mathrm{2}\right) \\ $$$$\mathrm{2}\left(\mathrm{3}−\sqrt{\mathrm{3}}\right)\mathrm{x}−\left(\mathrm{3}\sqrt{\mathrm{3}}−\mathrm{1}\right)\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)=\left(\mathrm{2}\sqrt{\mathrm{3}}−\mathrm{1}\right)\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right) \\ $$$$\left(\mathrm{6}−\mathrm{2}\sqrt{\mathrm{3}}\right)\mathrm{x}−\mathrm{3}\sqrt{\mathrm{3}}+\mathrm{1}+\left(\mathrm{3}\sqrt{\mathrm{3}}−\mathrm{1}\right)\mathrm{x}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{3}}+\mathrm{1}−\left(\mathrm{2}\sqrt{\mathrm{3}}−\mathrm{1}\right)\mathrm{x}^{\mathrm{2}} =\mathrm{0} \\ $$$$\sqrt{\mathrm{3}}\mathrm{x}^{\mathrm{2}} +\mathrm{2}\left(\mathrm{3}−\sqrt{\mathrm{3}}\right)\mathrm{x}−\left(\mathrm{5}\sqrt{\mathrm{3}}−\mathrm{2}\right)=\mathrm{0} \\ $$$$\boldsymbol{\mathrm{tan}\theta}=\boldsymbol{\mathrm{x}}_{\mathrm{1}} =\mathrm{1}.\mathrm{361080303}\Leftrightarrow\boldsymbol{\theta}\approx\mathrm{53}°\mathrm{41}'\mathrm{41} \\ $$$$\boldsymbol{\mathrm{tan}\theta}=\boldsymbol{\mathrm{x}}_{\mathrm{2}} =−\mathrm{2}.\mathrm{825181918}\Leftrightarrow\boldsymbol{\theta}\approx−\mathrm{70}°\mathrm{30}'\mathrm{30} \\ $$
Answered by bemath last updated on 11/Jul/20

Commented by floor(10²Eta[1]) last updated on 11/Jul/20

$$\mathrm{why}\:\mathrm{the}\:\mathrm{eq}.\:\mathrm{has}\:\mathrm{solution}\:\mathrm{if}\:\mathrm{that} \\ $$$$\mathrm{inequality}\:\mathrm{happens}? \\ $$
