Question Number 87492 by unknown last updated on 04/Apr/20
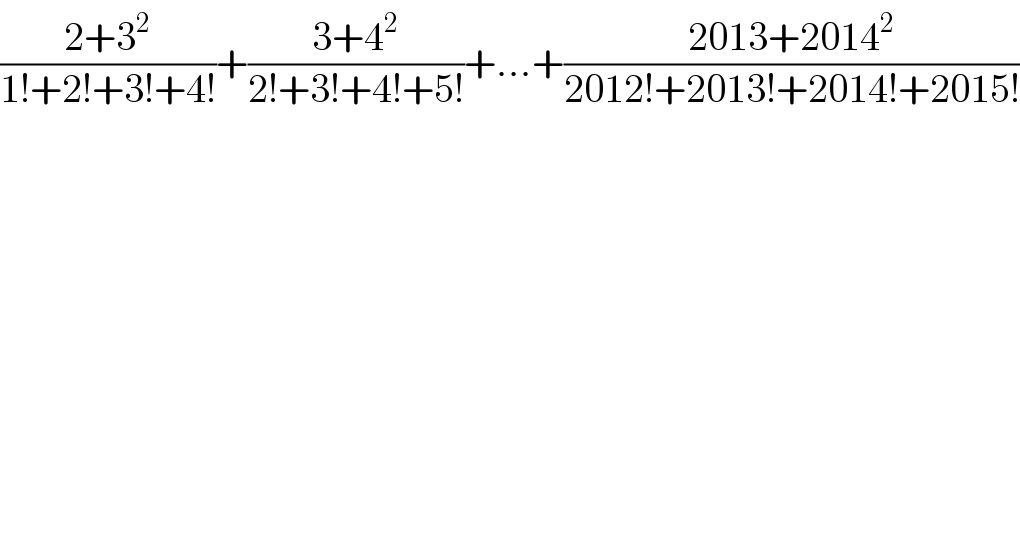
$$\frac{\mathrm{2}+\mathrm{3}^{\mathrm{2}} }{\mathrm{1}!+\mathrm{2}!+\mathrm{3}!+\mathrm{4}!}+\frac{\mathrm{3}+\mathrm{4}^{\mathrm{2}} }{\mathrm{2}!+\mathrm{3}!+\mathrm{4}!+\mathrm{5}!}+…+\frac{\mathrm{2013}+\mathrm{2014}^{\mathrm{2}} }{\mathrm{2012}!+\mathrm{2013}!+\mathrm{2014}!+\mathrm{2015}!} \\ $$
Answered by mind is power last updated on 04/Apr/20
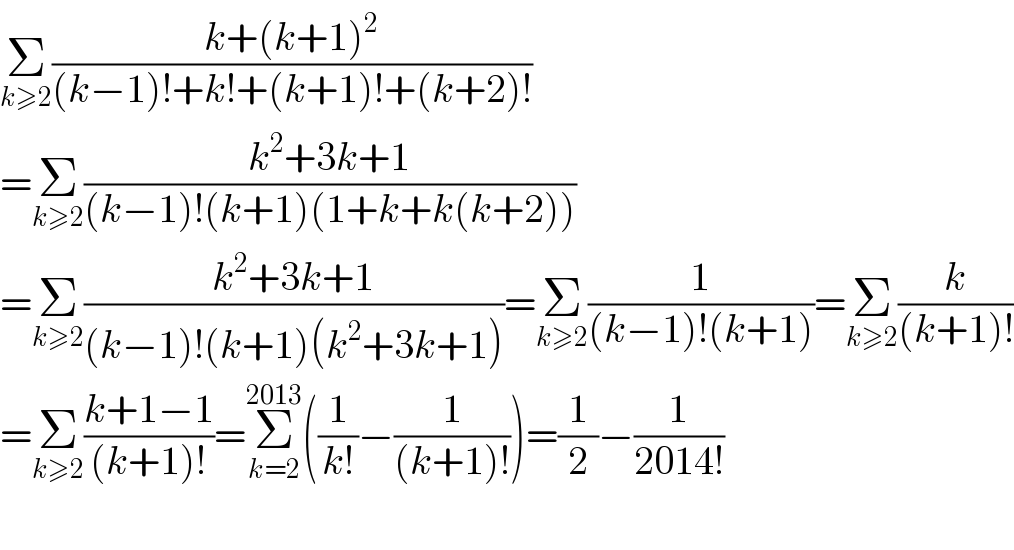
$$\underset{{k}\geqslant\mathrm{2}} {\sum}\frac{{k}+\left({k}+\mathrm{1}\right)^{\mathrm{2}} }{\left({k}−\mathrm{1}\right)!+{k}!+\left({k}+\mathrm{1}\right)!+\left({k}+\mathrm{2}\right)!} \\ $$$$=\underset{{k}\geqslant\mathrm{2}} {\sum}\frac{{k}^{\mathrm{2}} +\mathrm{3}{k}+\mathrm{1}}{\left({k}−\mathrm{1}\right)!\left({k}+\mathrm{1}\right)\left(\mathrm{1}+{k}+{k}\left({k}+\mathrm{2}\right)\right)} \\ $$$$=\underset{{k}\geqslant\mathrm{2}} {\sum}\frac{{k}^{\mathrm{2}} +\mathrm{3}{k}+\mathrm{1}}{\left({k}−\mathrm{1}\right)!\left({k}+\mathrm{1}\right)\left({k}^{\mathrm{2}} +\mathrm{3}{k}+\mathrm{1}\right)}=\underset{{k}\geqslant\mathrm{2}} {\sum}\frac{\mathrm{1}}{\left({k}−\mathrm{1}\right)!\left({k}+\mathrm{1}\right)}=\underset{{k}\geqslant\mathrm{2}} {\sum}\frac{{k}}{\left({k}+\mathrm{1}\right)!} \\ $$$$=\underset{{k}\geqslant\mathrm{2}} {\sum}\frac{{k}+\mathrm{1}−\mathrm{1}}{\left({k}+\mathrm{1}\right)!}=\underset{{k}=\mathrm{2}} {\overset{\mathrm{2013}} {\sum}}\left(\frac{\mathrm{1}}{{k}!}−\frac{\mathrm{1}}{\left({k}+\mathrm{1}\right)!}\right)=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2014}!} \\ $$$$ \\ $$
