Question Number 117391 by Dwaipayan Shikari last updated on 11/Oct/20
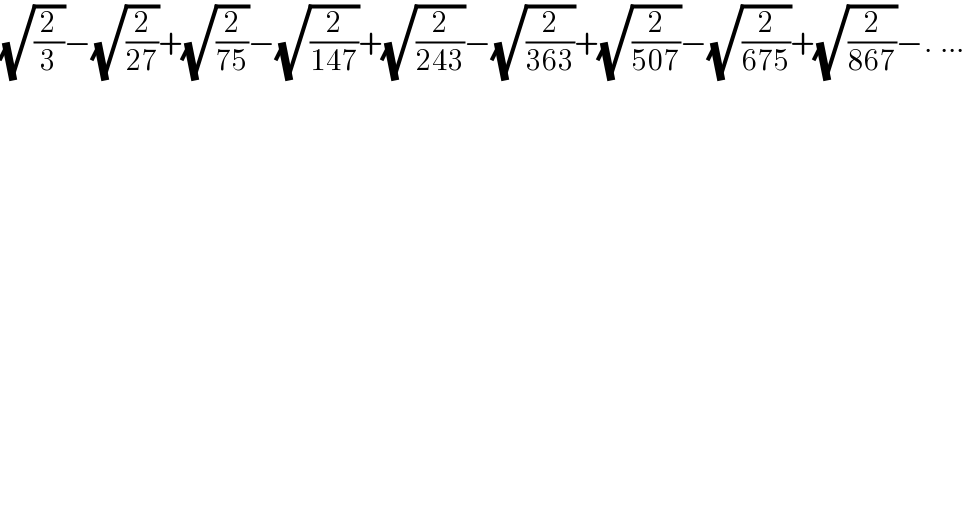
$$\sqrt{\frac{\mathrm{2}}{\mathrm{3}}}−\sqrt{\frac{\mathrm{2}}{\mathrm{27}}}+\sqrt{\frac{\mathrm{2}}{\mathrm{75}}}−\sqrt{\frac{\mathrm{2}}{\mathrm{147}}}+\sqrt{\frac{\mathrm{2}}{\mathrm{243}}}−\sqrt{\frac{\mathrm{2}}{\mathrm{363}}}+\sqrt{\frac{\mathrm{2}}{\mathrm{507}}}−\sqrt{\frac{\mathrm{2}}{\mathrm{675}}}+\sqrt{\frac{\mathrm{2}}{\mathrm{867}}}−._{} … \\ $$
Answered by Olaf last updated on 11/Oct/20
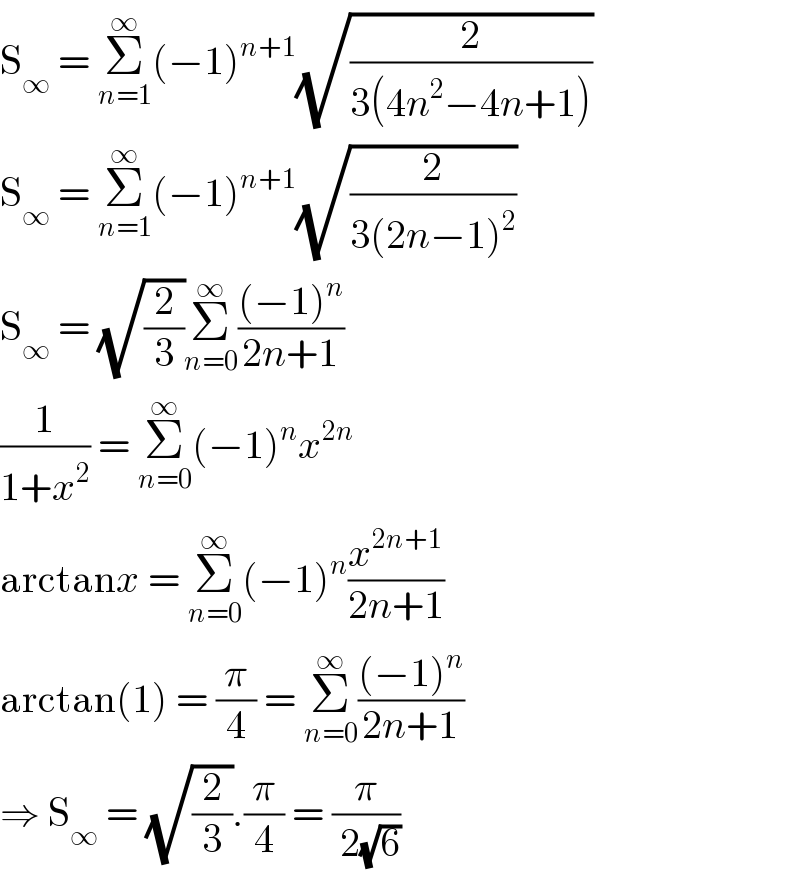
$$\mathrm{S}_{\infty} \:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \sqrt{\frac{\mathrm{2}}{\mathrm{3}\left(\mathrm{4}{n}^{\mathrm{2}} −\mathrm{4}{n}+\mathrm{1}\right)}} \\ $$$$\mathrm{S}_{\infty} \:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \sqrt{\frac{\mathrm{2}}{\mathrm{3}\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{2}} }} \\ $$$$\mathrm{S}_{\infty} \:=\:\sqrt{\frac{\mathrm{2}}{\mathrm{3}}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{1}} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} {x}^{\mathrm{2}{n}} \\ $$$$\mathrm{arctan}{x}\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \frac{{x}^{\mathrm{2}{n}+\mathrm{1}} }{\mathrm{2}{n}+\mathrm{1}} \\ $$$$\mathrm{arctan}\left(\mathrm{1}\right)\:=\:\frac{\pi}{\mathrm{4}}\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{1}} \\ $$$$\Rightarrow\:\mathrm{S}_{\infty} \:=\:\sqrt{\frac{\mathrm{2}}{\mathrm{3}}}.\frac{\pi}{\mathrm{4}}\:=\:\frac{\pi}{\:\mathrm{2}\sqrt{\mathrm{6}}} \\ $$
Commented by Dwaipayan Shikari last updated on 11/Oct/20

$${Great}\:{sir}! \\ $$
