Menu Close

2-3-2-3-4-3-3-5-4-3-6-5-3-

Tinku Tara 0 Comments
Pin




Question Number 130109 by Adel last updated on 22/Jan/21
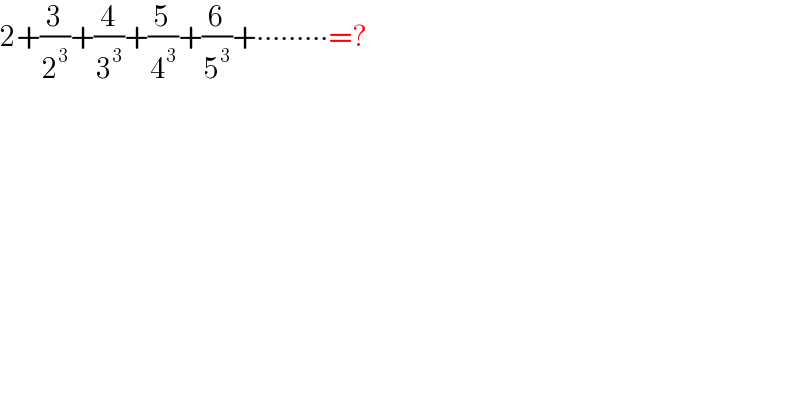
2+(3/2^3 )+(4/3^3 )+(5/4^3 )+(6/5^3 )+∙∙∙∙∙∙∙∙∙=?
$$\mathrm{2}+\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{3}} }+\frac{\mathrm{4}}{\mathrm{3}^{\mathrm{3}} }+\frac{\mathrm{5}}{\mathrm{4}^{\mathrm{3}} }+\frac{\mathrm{6}}{\mathrm{5}^{\mathrm{3}} }+\centerdot\centerdot\centerdot\centerdot\centerdot\centerdot\centerdot\centerdot\centerdot=? \\ $$
Answered by Olaf last updated on 22/Jan/21
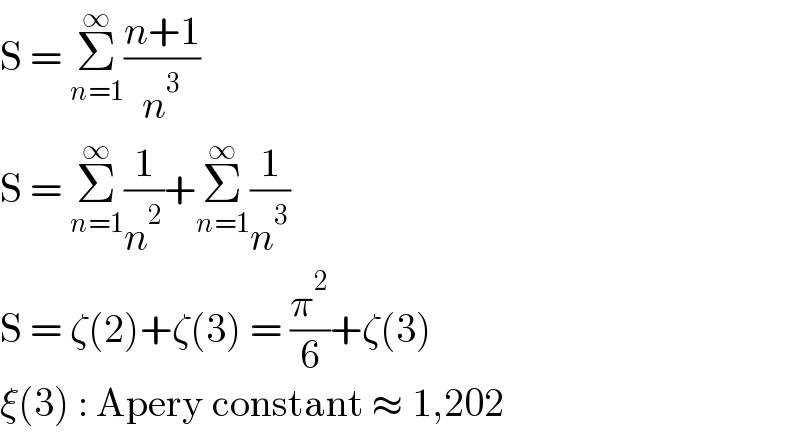
S = Σ_(n=1) ^∞ ((n+1)/n^3 ) S = Σ_(n=1) ^∞ (1/n^2 )+Σ_(n=1) ^∞ (1/n^3 ) S = ζ(2)+ζ(3) = (π^2 /6)+ζ(3) ξ(3) : Apery constant ≈ 1,202
$$\mathrm{S}\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{n}+\mathrm{1}}{{n}^{\mathrm{3}} } \\ $$$$\mathrm{S}\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} }+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{3}} } \\ $$$$\mathrm{S}\:=\:\zeta\left(\mathrm{2}\right)+\zeta\left(\mathrm{3}\right)\:=\:\frac{\pi^{\mathrm{2}} }{\mathrm{6}}+\zeta\left(\mathrm{3}\right) \\ $$$$\xi\left(\mathrm{3}\right)\::\:\mathrm{Apery}\:\mathrm{constant}\:\approx\:\mathrm{1},\mathrm{202} \\ $$
Commented by Adel last updated on 22/Jan/21
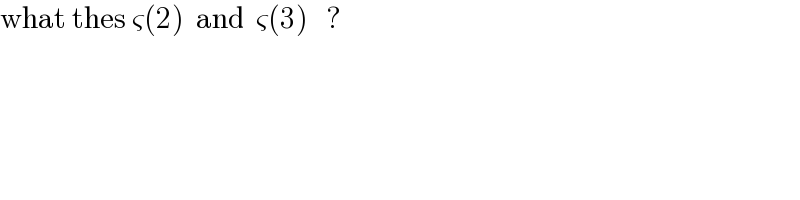
what thes ς(2) and ς(3) ?
$$\mathrm{what}\:\mathrm{thes}\:\varsigma\left(\mathrm{2}\right)\:\:\mathrm{and}\:\:\varsigma\left(\mathrm{3}\right)\:\:\:? \\ $$
Commented by Ar Brandon last updated on 22/Jan/21
ζ(n)=Σ_(k=1) ^∞ (1/k^n )
$$\zeta\left(\mathrm{n}\right)=\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{k}^{\mathrm{n}} } \\ $$
Commented by Olaf last updated on 22/Jan/21
ζ(s) = Σ_(n=1) ^∞ (1/n^s ) ζ(s) = Riemann zeta function. For some values of s it′s known. For example ζ(2) = (π^2 /6), ζ(4) = (π^4 /(90)) But for some values of s it′s approximative. For example ζ(3) = Σ_(n=1) ^∞ (1/n^3 ) ≈ 1,202056903.
$$\zeta\left({s}\right)\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{{s}} } \\ $$$$\zeta\left({s}\right)\:=\:\mathrm{Riemann}\:\mathrm{zeta}\:\mathrm{function}. \\ $$$$\mathrm{For}\:\mathrm{some}\:\mathrm{values}\:\mathrm{of}\:{s}\:\mathrm{it}'\mathrm{s}\:\mathrm{known}. \\ $$$$\mathrm{For}\:\mathrm{example}\:\zeta\left(\mathrm{2}\right)\:=\:\frac{\pi^{\mathrm{2}} }{\mathrm{6}},\:\zeta\left(\mathrm{4}\right)\:=\:\frac{\pi^{\mathrm{4}} }{\mathrm{90}} \\ $$$$\mathrm{But}\:\mathrm{for}\:\mathrm{some}\:\mathrm{values}\:\mathrm{of}\:{s}\:\mathrm{it}'\mathrm{s}\:\mathrm{approximative}. \\ $$$$\mathrm{For}\:\mathrm{example}\:\zeta\left(\mathrm{3}\right)\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{3}} }\:\approx\:\mathrm{1},\mathrm{202056903}. \\ $$
Commented by talminator2856791 last updated on 22/Jan/21
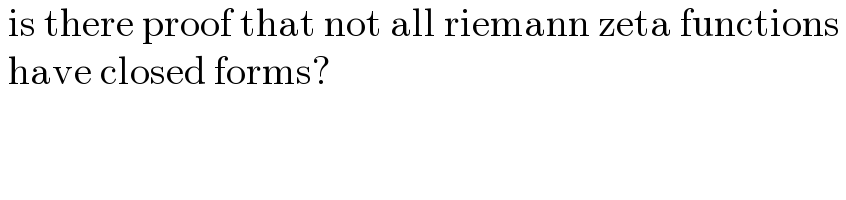
is there proof that not all riemann zeta functions have closed forms?
$$\:\mathrm{is}\:\mathrm{there}\:\mathrm{proof}\:\mathrm{that}\:\mathrm{not}\:\mathrm{all}\:\mathrm{riemann}\:\mathrm{zeta}\:\mathrm{functions}\: \\ $$$$\:\mathrm{have}\:\mathrm{closed}\:\mathrm{forms}? \\ $$
Answered by Ar Brandon last updated on 22/Jan/21
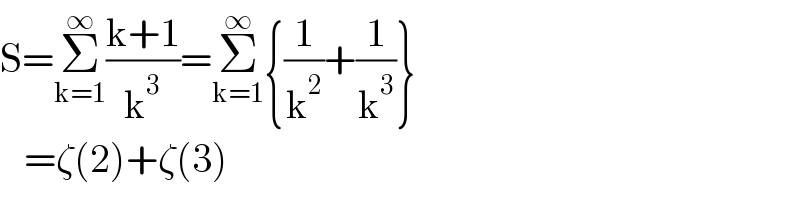
S=Σ_(k=1) ^∞ ((k+1)/k^3 )=Σ_(k=1) ^∞ {(1/k^2 )+(1/k^3 )} =ζ(2)+ζ(3)
$$\mathrm{S}=\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{k}+\mathrm{1}}{\mathrm{k}^{\mathrm{3}} }=\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\sum}}\left\{\frac{\mathrm{1}}{\mathrm{k}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{k}^{\mathrm{3}} }\right\} \\ $$$$\:\:\:=\zeta\left(\mathrm{2}\right)+\zeta\left(\mathrm{3}\right) \\ $$
Answered by Dwaipayan Shikari last updated on 22/Jan/21
Approximation of Σ_(n=1) ^∞ (1/n^3 ) f(x)=(1/x^3 ) Σ_(n=1) ^∞ (1/n^3 )=lim_(z→∞) ∫_1 ^∞ (1/x^3 )+((f(z)+f(1))/2)+Σ_(n=1) ^∞ (B_(2n) /((2n)!))(f^(2k−1) (z)−f^(2k−1) (1)) =(1/2)+(1/2)+(((3B_2 )/(2!))+((3.4.5)/(4!))B_4 +((3.4.5.6.7)/(6!))B_6 +((3.4.5.6.7.8.9)/(8!))B_8 +...) =1.2020.... (B_n =Bernoulli number) Even zeta function ζ(2n) (n∈Z) ζ(2)=(π^2 /6) ,ζ(4)=(π^4 /(90)),ζ(6)=(π^6 /(945)) ,ζ(8)=(π^8 /(9450)) ,ζ(10)=(π^(10) /(93555))....
$${Approximation}\:{of}\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{3}} } \\ $$$${f}\left({x}\right)=\frac{\mathrm{1}}{{x}^{\mathrm{3}} } \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{3}} }=\underset{{z}\rightarrow\infty} {\mathrm{lim}}\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{1}}{{x}^{\mathrm{3}} }+\frac{{f}\left({z}\right)+{f}\left(\mathrm{1}\right)}{\mathrm{2}}+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{B}_{\mathrm{2}{n}} }{\left(\mathrm{2}{n}\right)!}\left({f}^{\mathrm{2}{k}−\mathrm{1}} \left({z}\right)−{f}^{\mathrm{2}{k}−\mathrm{1}} \left(\mathrm{1}\right)\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}+\left(\frac{\mathrm{3}{B}_{\mathrm{2}} }{\mathrm{2}!}+\frac{\mathrm{3}.\mathrm{4}.\mathrm{5}}{\mathrm{4}!}{B}_{\mathrm{4}} +\frac{\mathrm{3}.\mathrm{4}.\mathrm{5}.\mathrm{6}.\mathrm{7}}{\mathrm{6}!}{B}_{\mathrm{6}} +\frac{\mathrm{3}.\mathrm{4}.\mathrm{5}.\mathrm{6}.\mathrm{7}.\mathrm{8}.\mathrm{9}}{\mathrm{8}!}{B}_{\mathrm{8}} +…\right) \\ $$$$=\mathrm{1}.\mathrm{2020}….\:\:\:\left({B}_{{n}} ={Bernoulli}\:{number}\right) \\ $$$${Even}\:{zeta}\:{function}\:\zeta\left(\mathrm{2}{n}\right)\:\:\left({n}\in\mathbb{Z}\right) \\ $$$$\zeta\left(\mathrm{2}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:,\zeta\left(\mathrm{4}\right)=\frac{\pi^{\mathrm{4}} }{\mathrm{90}},\zeta\left(\mathrm{6}\right)=\frac{\pi^{\mathrm{6}} }{\mathrm{945}}\:,\zeta\left(\mathrm{8}\right)=\frac{\pi^{\mathrm{8}} }{\mathrm{9450}}\:\:,\zeta\left(\mathrm{10}\right)=\frac{\pi^{\mathrm{10}} }{\mathrm{93555}}…. \\ $$
Commented by Adel last updated on 23/Jan/21
thanks bro
$$\mathrm{thanks}\:\mathrm{bro} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *