Question Number 102539 by Dwaipayan Shikari last updated on 09/Jul/20
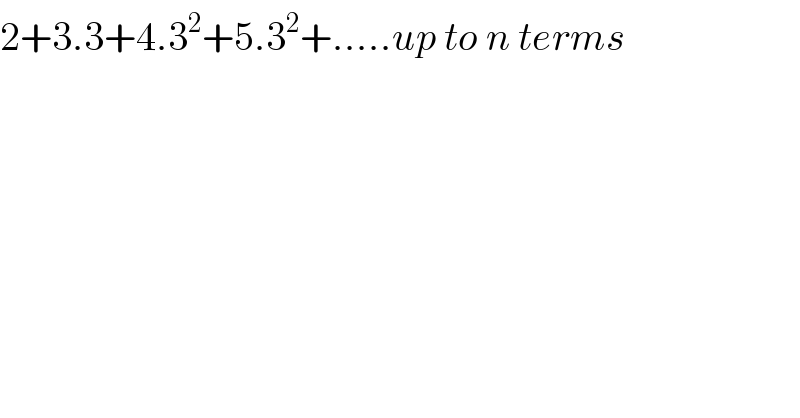
$$\mathrm{2}+\mathrm{3}.\mathrm{3}+\mathrm{4}.\mathrm{3}^{\mathrm{2}} +\mathrm{5}.\mathrm{3}^{\mathrm{2}} +…..{up}\:{to}\:{n}\:{terms} \\ $$
Commented by Dwaipayan Shikari last updated on 09/Jul/20
$${Thanking}\:{both}\:{of}\:{you} \\ $$
Commented by Rasheed.Sindhi last updated on 10/Jul/20
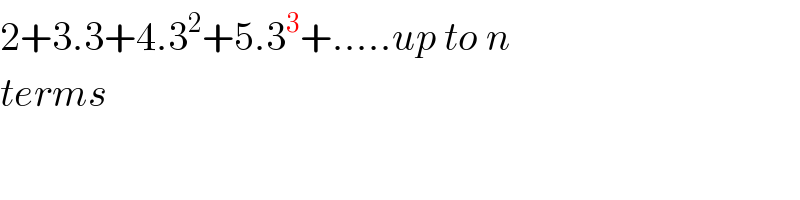
$$\mathrm{2}+\mathrm{3}.\mathrm{3}+\mathrm{4}.\mathrm{3}^{\mathrm{2}} +\mathrm{5}.\mathrm{3}^{\mathrm{3}} +…..{up}\:{to}\:{n} \\ $$$${terms} \\ $$
Answered by PRITHWISH SEN 2 last updated on 09/Jul/20

$$\mathrm{t}_{\mathrm{n}} =\:\left(\mathrm{n}+\mathrm{1}\right)\mathrm{3}^{\mathrm{n}−\mathrm{1}} =\:\mathrm{n3}^{\mathrm{n}−\mathrm{1}} +\mathrm{3}^{\mathrm{n}−\mathrm{1}} \\ $$$$\mathrm{t}_{\mathrm{1}} =\:\mathrm{1}.\mathrm{3}^{\mathrm{0}} +\:\mathrm{3}^{\mathrm{0}} \\ $$$$\mathrm{t}_{\mathrm{2}} \:=\:\mathrm{2}.\mathrm{3}^{\mathrm{1}} +\:\mathrm{3}^{\mathrm{1}} \\ $$$$\mathrm{t}_{\mathrm{3}} =\:\mathrm{3}.\mathrm{3}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} \\ $$$$……………… \\ $$$$\mathrm{t}_{\mathrm{n}} =\:\mathrm{n}.\mathrm{3}^{\mathrm{n}−\mathrm{1}} +\mathrm{3}^{\mathrm{n}−\mathrm{1}} \\ $$$$\boldsymbol{\mathrm{S}}_{\boldsymbol{\mathrm{n}}} =\:\frac{\mathrm{1}−\left(\mathrm{1}+\boldsymbol{\mathrm{n}}\right)\mathrm{3}^{\boldsymbol{\mathrm{n}}} }{\mathrm{1}−\mathrm{3}}+\frac{\mathrm{3}\left(\mathrm{1}−\mathrm{3}^{\boldsymbol{\mathrm{n}}} \right)}{\left(\mathrm{1}−\mathrm{3}\right)^{\mathrm{2}} }\:+\:\frac{\mathrm{3}^{\boldsymbol{\mathrm{n}}} −\mathrm{1}}{\mathrm{2}} \\ $$$$\:\:=\:\mathrm{3}^{\boldsymbol{\mathrm{n}}} \frac{\boldsymbol{\mathrm{n}}}{\mathrm{2}}+\frac{\mathrm{3}^{\boldsymbol{\mathrm{n}}} }{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{4}}\:\:\:\:\:\boldsymbol{\mathrm{please}}\:\boldsymbol{\mathrm{check}}. \\ $$
Answered by mr W last updated on 09/Jul/20
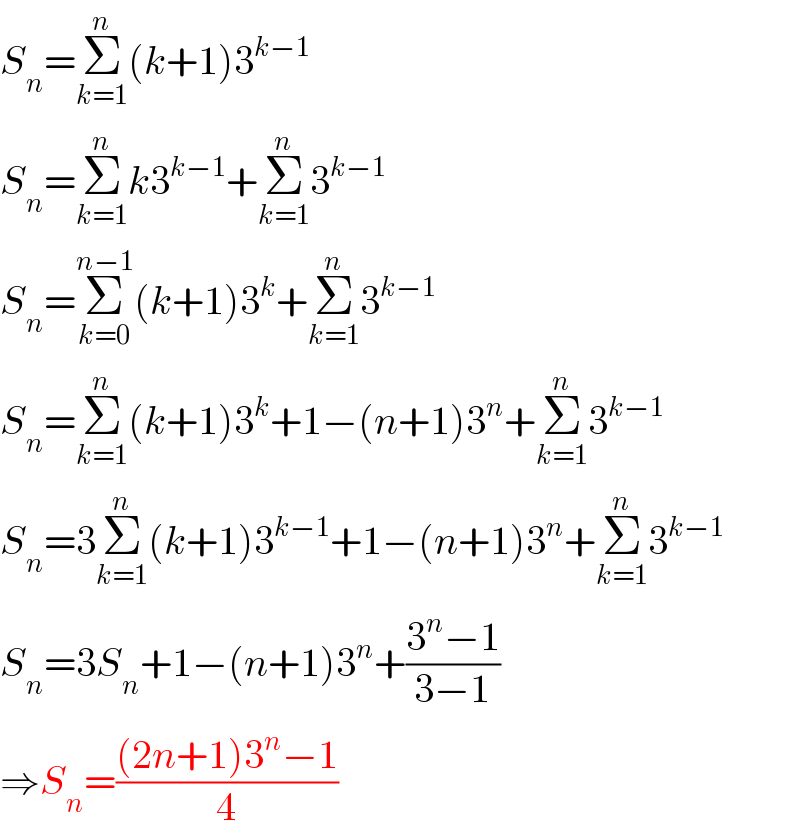
$${S}_{{n}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left({k}+\mathrm{1}\right)\mathrm{3}^{{k}−\mathrm{1}} \\ $$$${S}_{{n}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}\mathrm{3}^{{k}−\mathrm{1}} +\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{3}^{{k}−\mathrm{1}} \\ $$$${S}_{{n}} =\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\left({k}+\mathrm{1}\right)\mathrm{3}^{{k}} +\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{3}^{{k}−\mathrm{1}} \\ $$$${S}_{{n}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left({k}+\mathrm{1}\right)\mathrm{3}^{{k}} +\mathrm{1}−\left({n}+\mathrm{1}\right)\mathrm{3}^{{n}} +\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{3}^{{k}−\mathrm{1}} \\ $$$${S}_{{n}} =\mathrm{3}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left({k}+\mathrm{1}\right)\mathrm{3}^{{k}−\mathrm{1}} +\mathrm{1}−\left({n}+\mathrm{1}\right)\mathrm{3}^{{n}} +\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{3}^{{k}−\mathrm{1}} \\ $$$${S}_{{n}} =\mathrm{3}{S}_{{n}} +\mathrm{1}−\left({n}+\mathrm{1}\right)\mathrm{3}^{{n}} +\frac{\mathrm{3}^{{n}} −\mathrm{1}}{\mathrm{3}−\mathrm{1}} \\ $$$$\Rightarrow{S}_{{n}} =\frac{\left(\mathrm{2}{n}+\mathrm{1}\right)\mathrm{3}^{{n}} −\mathrm{1}}{\mathrm{4}} \\ $$
Commented by Dwaipayan Shikari last updated on 09/Jul/20

$${Thanking}\:{both}\:{of}\:{you} \\ $$
Answered by Dwaipayan Shikari last updated on 09/Jul/20
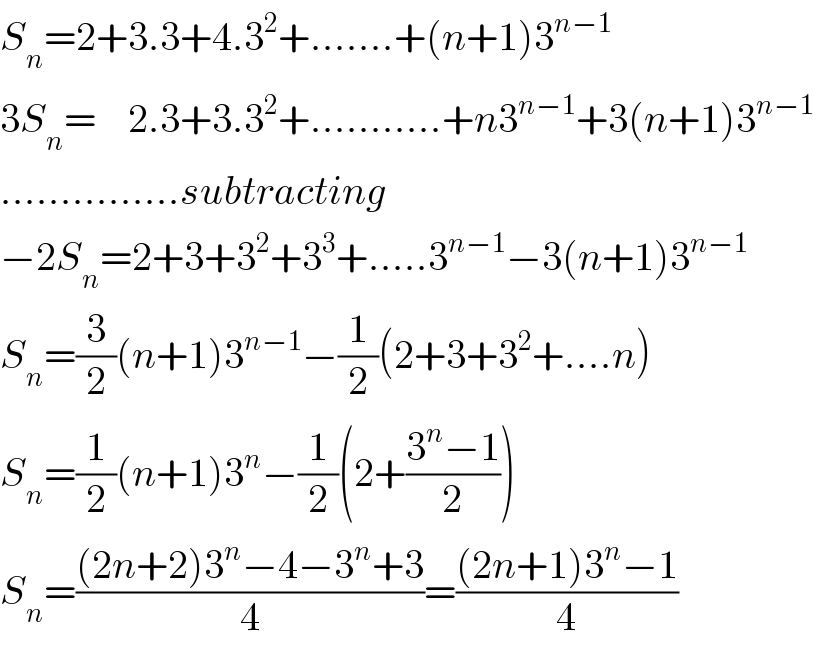
$${S}_{{n}} =\mathrm{2}+\mathrm{3}.\mathrm{3}+\mathrm{4}.\mathrm{3}^{\mathrm{2}} +…….+\left({n}+\mathrm{1}\right)\mathrm{3}^{{n}−\mathrm{1}} \\ $$$$\mathrm{3}{S}_{{n}} =\:\:\:\:\mathrm{2}.\mathrm{3}+\mathrm{3}.\mathrm{3}^{\mathrm{2}} +………..+{n}\mathrm{3}^{{n}−\mathrm{1}} +\mathrm{3}\left({n}+\mathrm{1}\right)\mathrm{3}^{{n}−\mathrm{1}} \\ $$$$……………{subtracting} \\ $$$$−\mathrm{2}{S}_{{n}} =\mathrm{2}+\mathrm{3}+\mathrm{3}^{\mathrm{2}} +\mathrm{3}^{\mathrm{3}} +…..\mathrm{3}^{{n}−\mathrm{1}} −\mathrm{3}\left({n}+\mathrm{1}\right)\mathrm{3}^{{n}−\mathrm{1}} \\ $$$${S}_{{n}} =\frac{\mathrm{3}}{\mathrm{2}}\left({n}+\mathrm{1}\right)\mathrm{3}^{{n}−\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}+\mathrm{3}+\mathrm{3}^{\mathrm{2}} +….{n}\right) \\ $$$${S}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}\left({n}+\mathrm{1}\right)\mathrm{3}^{{n}} −\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}+\frac{\mathrm{3}^{{n}} −\mathrm{1}}{\mathrm{2}}\right) \\ $$$${S}_{{n}} =\frac{\left(\mathrm{2}{n}+\mathrm{2}\right)\mathrm{3}^{{n}} −\mathrm{4}−\mathrm{3}^{{n}} +\mathrm{3}}{\mathrm{4}}=\frac{\left(\mathrm{2}{n}+\mathrm{1}\right)\mathrm{3}^{{n}} −\mathrm{1}}{\mathrm{4}} \\ $$
