Menu Close

2-3-i-is-a-cubic-root-for-18-3-35i-find-the-other-2-cubic-roots-

Tinku Tara 0 Comments
Pin




Question Number 104973 by malwaan last updated on 25/Jul/20
2(√3) + i is a cubic root for 18(√3) + 35i find the other 2 cubic roots
$$\mathrm{2}\sqrt{\mathrm{3}}\:+\:\boldsymbol{{i}}\:\:\:{is}\:{a}\:{cubic}\:{root}\:{for} \\ $$$$\mathrm{18}\sqrt{\mathrm{3}}\:+\:\mathrm{35}\boldsymbol{{i}}\: \\ $$$$\boldsymbol{{find}}\:\:\boldsymbol{{the}}\:\boldsymbol{{other}}\:\mathrm{2}\:\boldsymbol{{cubic}}\:\boldsymbol{{roots}} \\ $$
Commented by malwaan last updated on 25/Jul/20
شكرا جزيلا سيدي الفاضل واذا كان لديك طريقة او لوحة مفاتيح لكتابة المعادلات والنهايات والتكاملات وغيرها باللغة العربية فاتمنى تساعدني مع فائق احترامي محمد علوان اليمن
Answered by Rasheed.Sindhi last updated on 25/Jul/20
Let a is a given cuberoot of x (say) ∴ x^3 =a^3 ⇒x^3 −a^3 =0 ⇒(x−a)(x^2 +ax+a^2 )=0 ⇒x−a=0 ∨ x^2 +ax+a^2 =0 x=a(given) ∨ x=((−a±(√(a^2 −4a^2 )))/2) x=((−a±ai(√3))/2)=a(((−1±i(√3))/2)) x=aω,aω^2 a=2(√3) + i→ x=(2(√3) + i)ω , (2(√3) + i)ω^2 (Other two cuberoots)
$${Let}\:{a}\:{is}\:{a}\:{given}\:{cuberoot}\:{of}\:{x} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left({say}\right) \\ $$$$\therefore\:{x}^{\mathrm{3}} ={a}^{\mathrm{3}} \Rightarrow{x}^{\mathrm{3}} −{a}^{\mathrm{3}} =\mathrm{0} \\ $$$$\Rightarrow\left({x}−{a}\right)\left({x}^{\mathrm{2}} +{ax}+{a}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\Rightarrow{x}−{a}=\mathrm{0}\:\vee\:{x}^{\mathrm{2}} +{ax}+{a}^{\mathrm{2}} =\mathrm{0} \\ $$$$\:\:{x}={a}\left({given}\right)\:\vee\:{x}=\frac{−{a}\pm\sqrt{{a}^{\mathrm{2}} −\mathrm{4}{a}^{\mathrm{2}} }}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{x}=\frac{−{a}\pm{ai}\sqrt{\mathrm{3}}}{\mathrm{2}}={a}\left(\frac{−\mathrm{1}\pm{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{x}={a}\omega,{a}\omega^{\mathrm{2}} \\ $$$${a}=\mathrm{2}\sqrt{\mathrm{3}}\:+\:\boldsymbol{{i}}\rightarrow \\ $$$${x}=\left(\mathrm{2}\sqrt{\mathrm{3}}\:+\:\boldsymbol{{i}}\right)\omega\:,\:\left(\mathrm{2}\sqrt{\mathrm{3}}\:+\:\boldsymbol{{i}}\right)\omega^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\left({Other}\:{two}\:{cuberoots}\right) \\ $$
Commented by malwaan last updated on 25/Jul/20
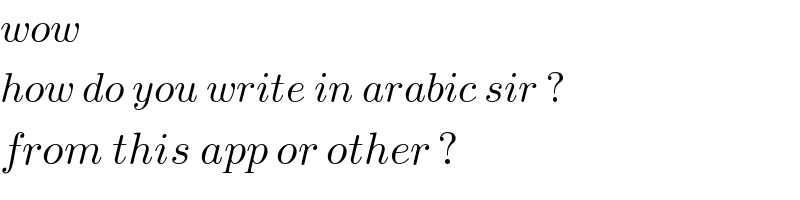
wow how do you write in arabic sir ? from this app or other ?
$${wow} \\ $$$${how}\:{do}\:{you}\:{write}\:{in}\:{arabic}\:{sir}\:? \\ $$$${from}\:{this}\:{app}\:{or}\:{other}\:? \\ $$
Commented by Rasheed.Sindhi last updated on 25/Jul/20
Use the option 'plain text comment' to write with your arabic keyboard: ل^۲+۸ل+۲۲=۷ √(8)=2√(2)
Commented by Rasheed.Sindhi last updated on 25/Jul/20
لا ريب يا سيدي!
Commented by malwaan last updated on 25/Jul/20
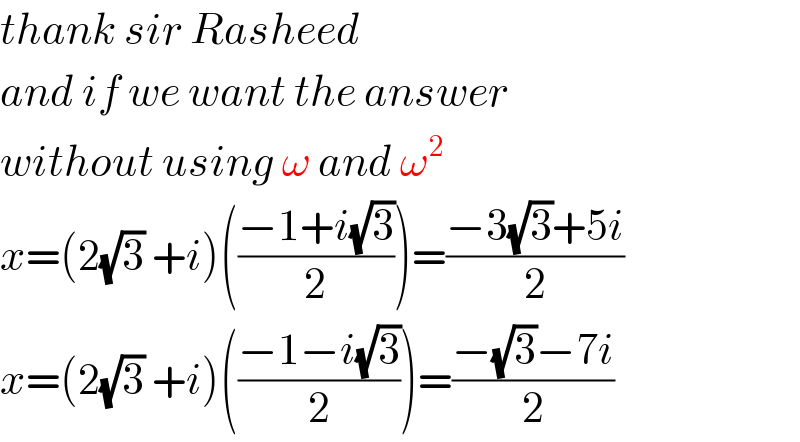
thank sir Rasheed and if we want the answer without using ω and ω^2 x=(2(√3) +i)(((−1+i(√3))/2))=((−3(√3)+5i)/2) x=(2(√3) +i)(((−1−i(√3))/2))=((−(√3)−7i)/2)
$${thank}\:{sir}\:{Rasheed} \\ $$$${and}\:{if}\:{we}\:{want}\:{the}\:{answer} \\ $$$${without}\:{using}\:\omega\:{and}\:\omega^{\mathrm{2}} \\ $$$${x}=\left(\mathrm{2}\sqrt{\mathrm{3}}\:+{i}\right)\left(\frac{−\mathrm{1}+{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\right)=\frac{−\mathrm{3}\sqrt{\mathrm{3}}+\mathrm{5}{i}}{\mathrm{2}} \\ $$$${x}=\left(\mathrm{2}\sqrt{\mathrm{3}}\:+{i}\right)\left(\frac{−\mathrm{1}−{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\right)=\frac{−\sqrt{\mathrm{3}}−\mathrm{7}{i}}{\mathrm{2}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *