Question Number 61566 by aliesam last updated on 04/Jun/19
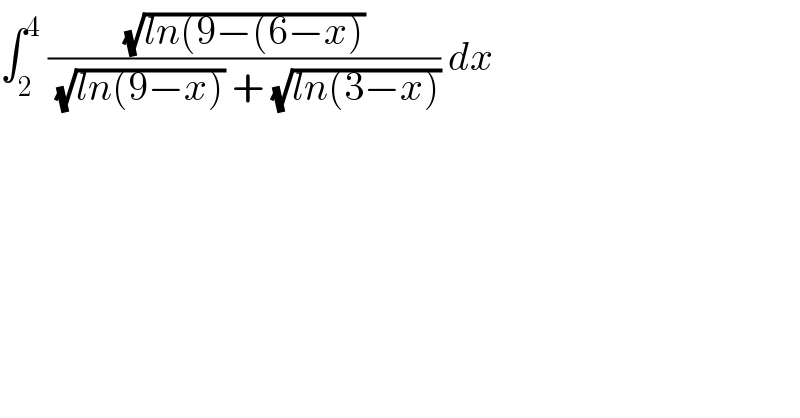
$$\int_{\mathrm{2}} ^{\mathrm{4}} \:\frac{\sqrt{{ln}\left(\mathrm{9}−\left(\mathrm{6}−{x}\right)\right.}}{\:\sqrt{{ln}\left(\mathrm{9}−{x}\right)}\:+\:\sqrt{{ln}\left(\mathrm{3}−{x}\right)}}\:{dx} \\ $$
Answered by tanmay last updated on 04/Jun/19
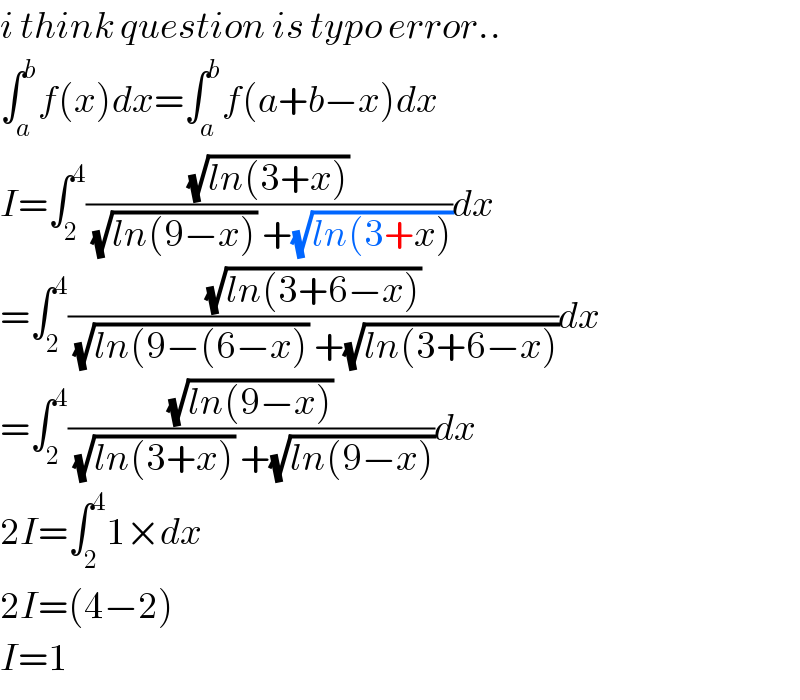
$${i}\:{think}\:{question}\:{is}\:{typo}\:{error}.. \\ $$$$\int_{{a}} ^{{b}} {f}\left({x}\right){dx}=\int_{{a}} ^{{b}} {f}\left({a}+{b}−{x}\right){dx} \\ $$$${I}=\int_{\mathrm{2}} ^{\mathrm{4}} \frac{\sqrt{{ln}\left(\mathrm{3}+{x}\right)}}{\:\sqrt{{ln}\left(\mathrm{9}−{x}\right)}\:+\sqrt{{ln}\left(\mathrm{3}+{x}\right)}}{dx} \\ $$$$=\int_{\mathrm{2}} ^{\mathrm{4}} \frac{\sqrt{{ln}\left(\mathrm{3}+\mathrm{6}−{x}\right)}}{\:\sqrt{{ln}\left(\mathrm{9}−\left(\mathrm{6}−{x}\right)\right.}\:+\sqrt{{ln}\left(\mathrm{3}+\mathrm{6}−{x}\right)}}{dx} \\ $$$$=\int_{\mathrm{2}} ^{\mathrm{4}} \frac{\sqrt{{ln}\left(\mathrm{9}−{x}\right)}}{\:\sqrt{{ln}\left(\mathrm{3}+{x}\right)}\:+\sqrt{{ln}\left(\mathrm{9}−{x}\right)}}{dx} \\ $$$$\mathrm{2}{I}=\int_{\mathrm{2}} ^{\mathrm{4}} \mathrm{1}×{dx} \\ $$$$\mathrm{2}{I}=\left(\mathrm{4}−\mathrm{2}\right) \\ $$$${I}=\mathrm{1} \\ $$
Commented by aliesam last updated on 04/Jun/19

$${yes}\:{thats}\:{right}\: \\ $$$${thank}\:{you}\:{sir} \\ $$
Commented by tanmay last updated on 04/Jun/19

$${most}\:{welcome}\:{sir} \\ $$
