Question Number 163720 by alcohol last updated on 09/Jan/22
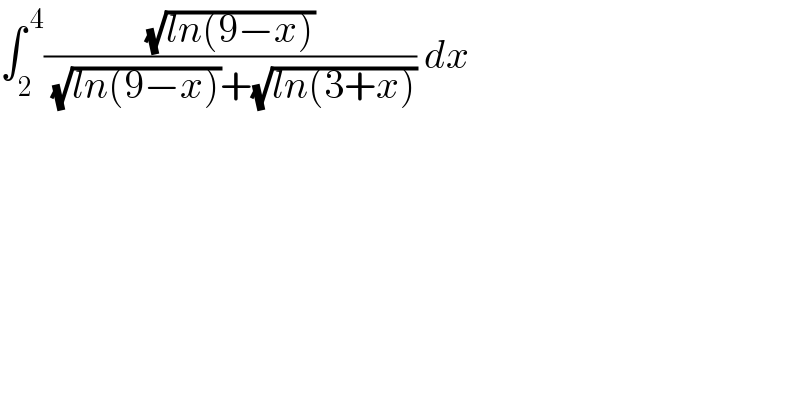
$$\int_{\mathrm{2}} ^{\:\mathrm{4}} \frac{\sqrt{{ln}\left(\mathrm{9}−{x}\right)}}{\:\sqrt{{ln}\left(\mathrm{9}−{x}\right)}+\sqrt{{ln}\left(\mathrm{3}+{x}\right)}}\:{dx} \\ $$$$ \\ $$
Answered by Mathspace last updated on 09/Jan/22
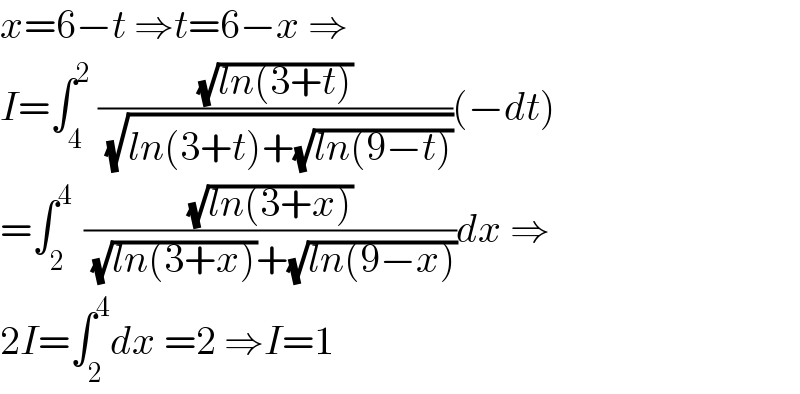
$${x}=\mathrm{6}−{t}\:\Rightarrow{t}=\mathrm{6}−{x}\:\Rightarrow \\ $$$${I}=\int_{\mathrm{4}} ^{\mathrm{2}} \:\frac{\sqrt{{ln}\left(\mathrm{3}+{t}\right)}}{\:\sqrt{{ln}\left(\mathrm{3}+{t}\right)+\sqrt{{ln}\left(\mathrm{9}−{t}\right)}}}\left(−{dt}\right) \\ $$$$=\int_{\mathrm{2}} ^{\mathrm{4}\:} \:\frac{\sqrt{{ln}\left(\mathrm{3}+{x}\right)}}{\:\sqrt{{ln}\left(\mathrm{3}+{x}\right)}+\sqrt{{ln}\left(\mathrm{9}−{x}\right)}}{dx}\:\Rightarrow \\ $$$$\mathrm{2}{I}=\int_{\mathrm{2}} ^{\mathrm{4}} {dx}\:=\mathrm{2}\:\Rightarrow{I}=\mathrm{1} \\ $$
Commented by peter frank last updated on 11/Jan/22

$$\mathrm{great} \\ $$
