Question Number 118753 by carlosmald last updated on 19/Oct/20

$$\int_{\mathrm{2}} ^{\mathrm{4}} {x}^{\mathrm{3}} {e}^{{x}} {dx} \\ $$
Commented by mohammad17 last updated on 19/Oct/20
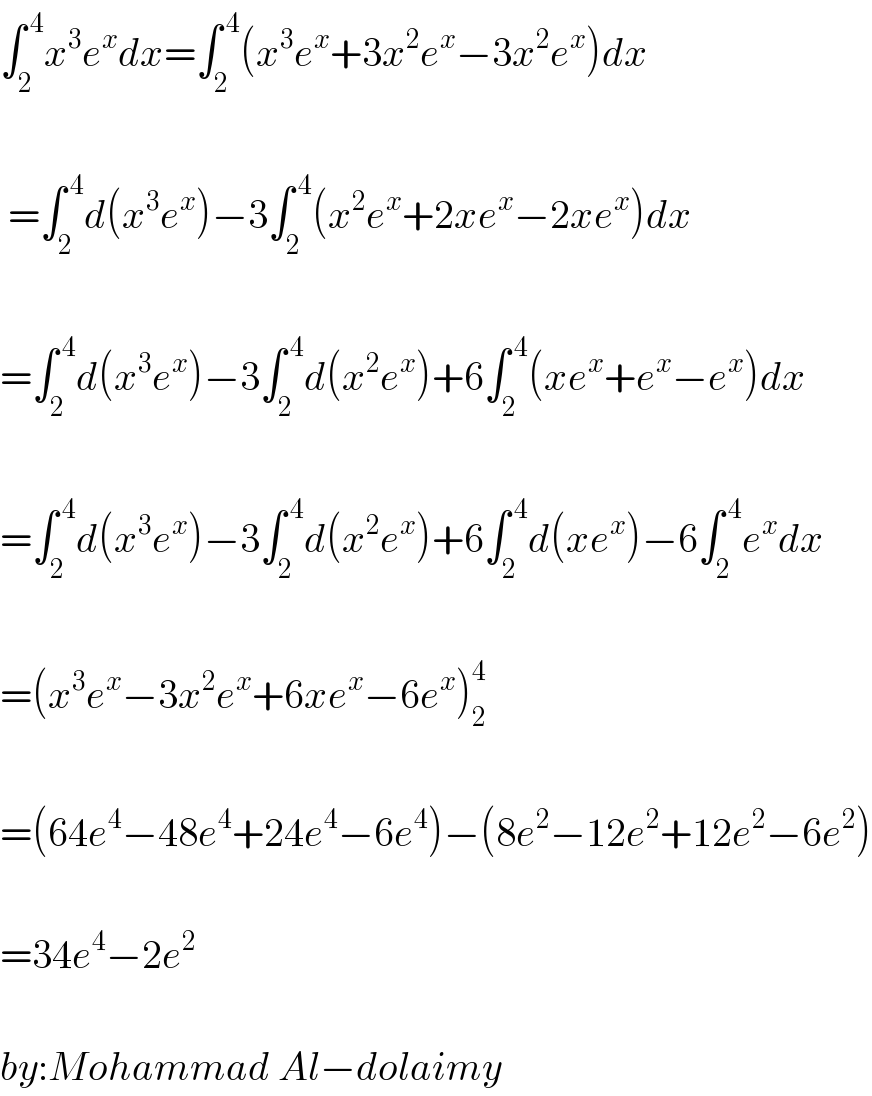
$$\int_{\mathrm{2}} ^{\:\mathrm{4}} {x}^{\mathrm{3}} {e}^{{x}} {dx}=\int_{\mathrm{2}} ^{\:\mathrm{4}} \left({x}^{\mathrm{3}} {e}^{{x}} +\mathrm{3}{x}^{\mathrm{2}} {e}^{{x}} −\mathrm{3}{x}^{\mathrm{2}} {e}^{{x}} \right){dx} \\ $$$$ \\ $$$$\:=\int_{\mathrm{2}} ^{\:\mathrm{4}} {d}\left({x}^{\mathrm{3}} {e}^{{x}} \right)−\mathrm{3}\int_{\mathrm{2}} ^{\:\mathrm{4}} \left({x}^{\mathrm{2}} {e}^{{x}} +\mathrm{2}{xe}^{{x}} −\mathrm{2}{xe}^{{x}} \right){dx} \\ $$$$ \\ $$$$=\int_{\mathrm{2}} ^{\:\mathrm{4}} {d}\left({x}^{\mathrm{3}} {e}^{{x}} \right)−\mathrm{3}\int_{\mathrm{2}} ^{\:\mathrm{4}} {d}\left({x}^{\mathrm{2}} {e}^{{x}} \right)+\mathrm{6}\int_{\mathrm{2}} ^{\:\mathrm{4}} \left({xe}^{{x}} +{e}^{{x}} −{e}^{{x}} \right){dx} \\ $$$$ \\ $$$$=\int_{\mathrm{2}} ^{\:\mathrm{4}} {d}\left({x}^{\mathrm{3}} {e}^{{x}} \right)−\mathrm{3}\int_{\mathrm{2}} ^{\:\mathrm{4}} {d}\left({x}^{\mathrm{2}} {e}^{{x}} \right)+\mathrm{6}\int_{\mathrm{2}} ^{\:\mathrm{4}} {d}\left({xe}^{{x}} \right)−\mathrm{6}\int_{\mathrm{2}} ^{\:\mathrm{4}} {e}^{{x}} {dx} \\ $$$$ \\ $$$$=\left({x}^{\mathrm{3}} {e}^{{x}} −\mathrm{3}{x}^{\mathrm{2}} {e}^{{x}} +\mathrm{6}{xe}^{{x}} −\mathrm{6}{e}^{{x}} \right)_{\mathrm{2}} ^{\mathrm{4}} \\ $$$$ \\ $$$$=\left(\mathrm{64}{e}^{\mathrm{4}} −\mathrm{48}{e}^{\mathrm{4}} +\mathrm{24}{e}^{\mathrm{4}} −\mathrm{6}{e}^{\mathrm{4}} \right)−\left(\mathrm{8}{e}^{\mathrm{2}} −\mathrm{12}{e}^{\mathrm{2}} +\mathrm{12}{e}^{\mathrm{2}} −\mathrm{6}{e}^{\mathrm{2}} \right) \\ $$$$ \\ $$$$=\mathrm{34}{e}^{\mathrm{4}} −\mathrm{2}{e}^{\mathrm{2}} \\ $$$$ \\ $$$${by}:{Mohammad}\:{Al}−{dolaimy} \\ $$
Answered by bemath last updated on 19/Oct/20
![by Tanzalin formula determinant (((x^3 e^x )),((3x^2 e^x (+))),((6x e^x (−))),((6 e^x (+))),((0 e^x (−)))) ∫ _2^3 x^3 e^x dx = [ x^3 e^x −3x^2 e^x +6xe^x −6e^x ]_2 ^3 = (e^x [x^3 −3x^2 +6x−6 ] )_2 ^3 = 12e^3 −2e^2](https://www.tinkutara.com/question/Q118755.png)
$$\:{by}\:{Tanzalin}\:{formula}\: \\ $$$$\:\begin{vmatrix}{{x}^{\mathrm{3}} \:\:\:\:\:{e}^{{x}} }\\{\mathrm{3}{x}^{\mathrm{2}} \:\:\:{e}^{{x}} \:\left(+\right)}\\{\mathrm{6}{x}\:\:\:\:\:{e}^{{x}} \:\:\left(−\right)}\\{\mathrm{6}\:\:\:\:\:\:\:\:{e}^{{x}} \:\left(+\right)}\\{\mathrm{0}\:\:\:\:\:\:\:{e}^{{x}} \:\:\left(−\right)}\end{vmatrix} \\ $$$$\int\:_{\mathrm{2}} ^{\mathrm{3}} \:{x}^{\mathrm{3}} \:{e}^{{x}} \:{dx}\:=\:\left[\:{x}^{\mathrm{3}} {e}^{{x}} −\mathrm{3}{x}^{\mathrm{2}} {e}^{{x}} +\mathrm{6}{xe}^{{x}} −\mathrm{6}{e}^{{x}} \:\right]_{\mathrm{2}} ^{\mathrm{3}} \\ $$$$=\:\left({e}^{{x}} \:\left[{x}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} +\mathrm{6}{x}−\mathrm{6}\:\right]\:\right)_{\mathrm{2}} ^{\mathrm{3}} \\ $$$$=\:\mathrm{12}{e}^{\mathrm{3}} −\mathrm{2}{e}^{\mathrm{2}} \: \\ $$
Answered by Dwaipayan Shikari last updated on 19/Oct/20
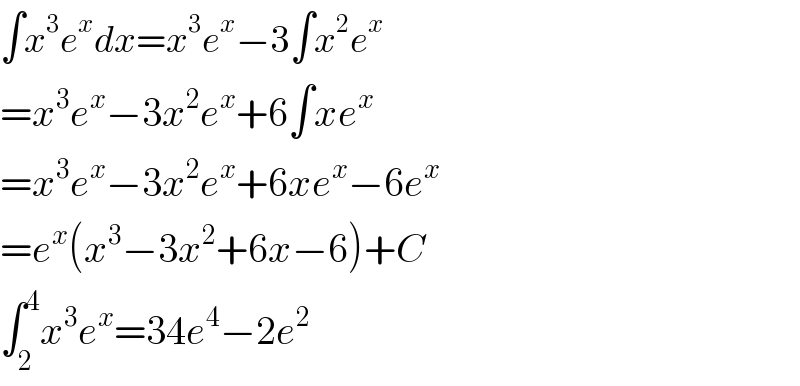
$$\int{x}^{\mathrm{3}} {e}^{{x}} {dx}={x}^{\mathrm{3}} {e}^{{x}} −\mathrm{3}\int{x}^{\mathrm{2}} {e}^{{x}} \\ $$$$={x}^{\mathrm{3}} {e}^{{x}} −\mathrm{3}{x}^{\mathrm{2}} {e}^{{x}} +\mathrm{6}\int{xe}^{{x}} \\ $$$$={x}^{\mathrm{3}} {e}^{{x}} −\mathrm{3}{x}^{\mathrm{2}} {e}^{{x}} +\mathrm{6}{xe}^{{x}} −\mathrm{6}{e}^{{x}} \\ $$$$={e}^{{x}} \left({x}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} +\mathrm{6}{x}−\mathrm{6}\right)+{C} \\ $$$$\int_{\mathrm{2}} ^{\mathrm{4}} {x}^{\mathrm{3}} {e}^{{x}} =\mathrm{34}{e}^{\mathrm{4}} −\mathrm{2}{e}^{\mathrm{2}} \\ $$
Answered by peter frank last updated on 19/Oct/20

$$\mathrm{by}\:\mathrm{part} \\ $$
