Question Number 129785 by bramlexs22 last updated on 19/Jan/21
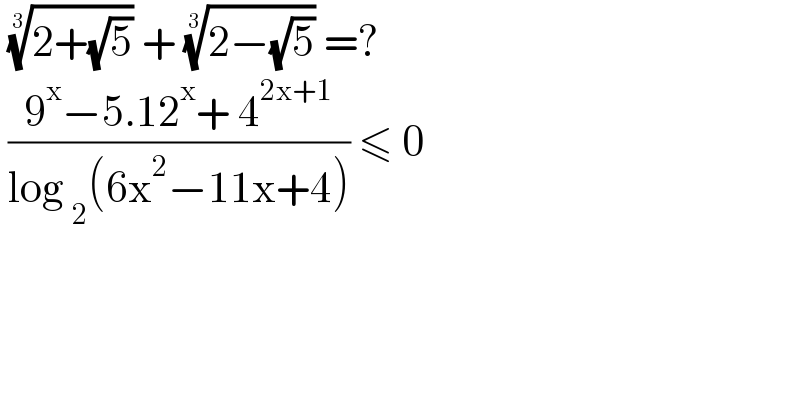
$$\:\sqrt[{\mathrm{3}}]{\mathrm{2}+\sqrt{\mathrm{5}}}\:+\:\sqrt[{\mathrm{3}}]{\mathrm{2}−\sqrt{\mathrm{5}}}\:=? \\ $$$$\:\frac{\mathrm{9}^{\mathrm{x}} −\mathrm{5}.\mathrm{12}^{\mathrm{x}} +\:\mathrm{4}^{\mathrm{2x}+\mathrm{1}} }{\mathrm{log}\:_{\mathrm{2}} \left(\mathrm{6x}^{\mathrm{2}} −\mathrm{11x}+\mathrm{4}\right)}\:\leqslant\:\mathrm{0}\: \\ $$
Answered by EDWIN88 last updated on 19/Jan/21
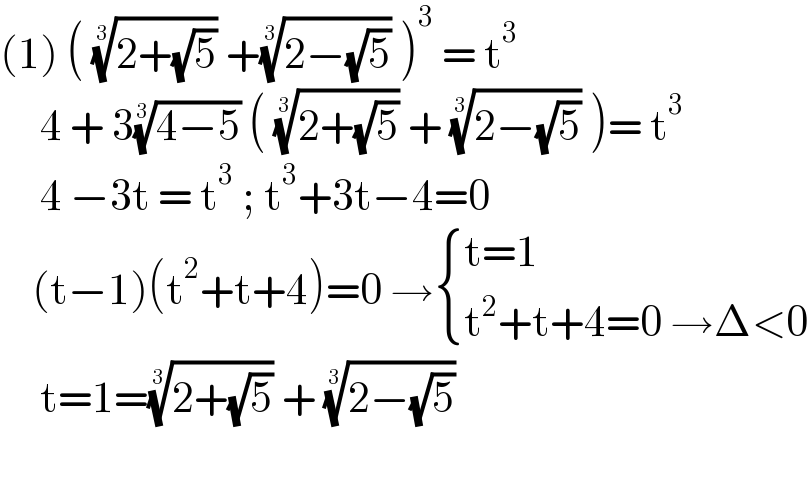
$$\left(\mathrm{1}\right)\:\left(\:\sqrt[{\mathrm{3}}]{\mathrm{2}+\sqrt{\mathrm{5}}}\:+\sqrt[{\mathrm{3}}]{\mathrm{2}−\sqrt{\mathrm{5}}}\:\right)^{\mathrm{3}} \:=\:\mathrm{t}^{\mathrm{3}} \\ $$$$\:\:\:\:\:\mathrm{4}\:+\:\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{4}−\mathrm{5}}\:\left(\:\sqrt[{\mathrm{3}}]{\mathrm{2}+\sqrt{\mathrm{5}}}\:+\:\sqrt[{\mathrm{3}}]{\mathrm{2}−\sqrt{\mathrm{5}}}\:\right)=\:\mathrm{t}^{\mathrm{3}} \\ $$$$\:\:\:\:\:\mathrm{4}\:−\mathrm{3t}\:=\:\mathrm{t}^{\mathrm{3}} \:;\:\mathrm{t}^{\mathrm{3}} +\mathrm{3t}−\mathrm{4}=\mathrm{0} \\ $$$$\:\:\:\:\left(\mathrm{t}−\mathrm{1}\right)\left(\mathrm{t}^{\mathrm{2}} +\mathrm{t}+\mathrm{4}\right)=\mathrm{0}\:\rightarrow\begin{cases}{\mathrm{t}=\mathrm{1}}\\{\mathrm{t}^{\mathrm{2}} +\mathrm{t}+\mathrm{4}=\mathrm{0}\:\rightarrow\Delta<\mathrm{0}}\end{cases} \\ $$$$\:\:\:\:\:\mathrm{t}=\mathrm{1}=\sqrt[{\mathrm{3}}]{\mathrm{2}+\sqrt{\mathrm{5}}}\:+\:\sqrt[{\mathrm{3}}]{\mathrm{2}−\sqrt{\mathrm{5}}}\: \\ $$$$\:\:\:\:\: \\ $$
