Question Number 37692 by kunal1234523 last updated on 16/Jun/18
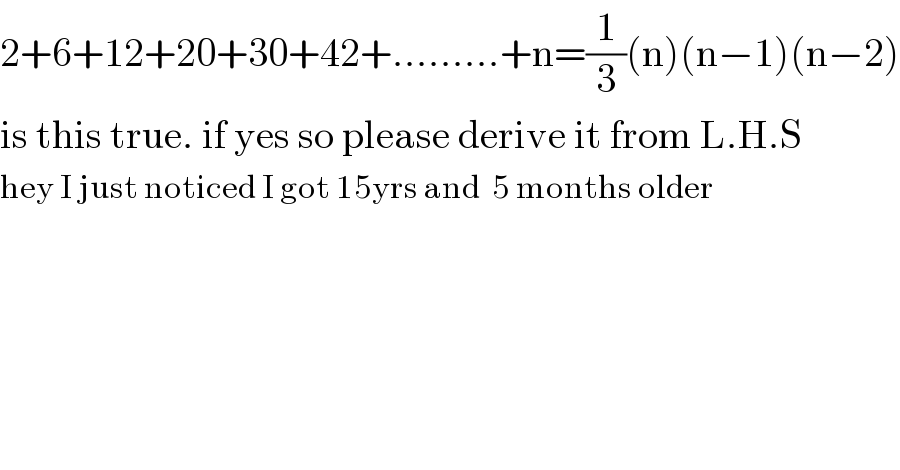
$$\mathrm{2}+\mathrm{6}+\mathrm{12}+\mathrm{20}+\mathrm{30}+\mathrm{42}+………+\mathrm{n}=\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{n}\right)\left(\mathrm{n}−\mathrm{1}\right)\left(\mathrm{n}−\mathrm{2}\right) \\ $$$$\mathrm{is}\:\mathrm{this}\:\mathrm{true}.\:\mathrm{if}\:\mathrm{yes}\:\mathrm{so}\:\mathrm{please}\:\mathrm{derive}\:\mathrm{it}\:\mathrm{from}\:\mathrm{L}.\mathrm{H}.\mathrm{S} \\ $$$$\mathrm{hey}\:\mathrm{I}\:\mathrm{just}\:\mathrm{noticed}\:\mathrm{I}\:\mathrm{got}\:\mathrm{15yrs}\:\mathrm{and}\:\:\mathrm{5}\:\mathrm{months}\:\mathrm{older} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 16/Jun/18
![s=2+6+12+20+30+42+...+T_(n−1) +T_n s= 2+6+12+20+......+T_(n−2) +T_(n−1) +T_n shifting right and substructing 0=2+4+6+8+10+...+(−T_n ) T_n =2+4+6+8...upto n terms T_n =(n/2)[2×2+(n−1)×2 T_n =(n/2)[4+2n−2] T_n =(n/2)[2n+2] T_n =n^2 +n s=Σ_1 ^n n^2 +Σ_1 ^n n s=((n(n+1)(2n+1))/6)+((n(n+1))/2) s=((n(n+1))/2)(((2n+1)/3)+1) s=((n(n+1))/2)(((2n+4)/3)) =((n(n+1)(n+2))/3)](https://www.tinkutara.com/question/Q37698.png)
$${s}=\mathrm{2}+\mathrm{6}+\mathrm{12}+\mathrm{20}+\mathrm{30}+\mathrm{42}+…+{T}_{{n}−\mathrm{1}} +{T}_{{n}} \\ $$$${s}=\:\:\:\:\:\:\:\mathrm{2}+\mathrm{6}+\mathrm{12}+\mathrm{20}+……+{T}_{{n}−\mathrm{2}} +{T}_{{n}−\mathrm{1}} +{T}_{{n}} \\ $$$${shifting}\:{right}\:{and}\:{substructing} \\ $$$$\mathrm{0}=\mathrm{2}+\mathrm{4}+\mathrm{6}+\mathrm{8}+\mathrm{10}+…+\left(−{T}_{{n}} \right) \\ $$$${T}_{{n}} =\mathrm{2}+\mathrm{4}+\mathrm{6}+\mathrm{8}…{upto}\:{n}\:{terms} \\ $$$${T}_{{n}} =\frac{{n}}{\mathrm{2}}\left[\mathrm{2}×\mathrm{2}+\left({n}−\mathrm{1}\right)×\mathrm{2}\right. \\ $$$${T}_{{n}} =\frac{{n}}{\mathrm{2}}\left[\mathrm{4}+\mathrm{2}{n}−\mathrm{2}\right] \\ $$$${T}_{{n}} =\frac{{n}}{\mathrm{2}}\left[\mathrm{2}{n}+\mathrm{2}\right] \\ $$$${T}_{{n}} ={n}^{\mathrm{2}} +{n} \\ $$$${s}=\underset{\mathrm{1}} {\overset{{n}} {\sum}}{n}^{\mathrm{2}} +\underset{\mathrm{1}} {\overset{{n}} {\sum}}{n} \\ $$$${s}=\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{6}}+\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}} \\ $$$${s}=\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}\left(\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{3}}+\mathrm{1}\right) \\ $$$${s}=\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}\left(\frac{\mathrm{2}{n}+\mathrm{4}}{\mathrm{3}}\right) \\ $$$$=\frac{{n}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}{\mathrm{3}} \\ $$$$ \\ $$$$ \\ $$
Commented by kunal1234523 last updated on 17/Jun/18
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{sir} \\ $$
Answered by ajfour last updated on 16/Jun/18
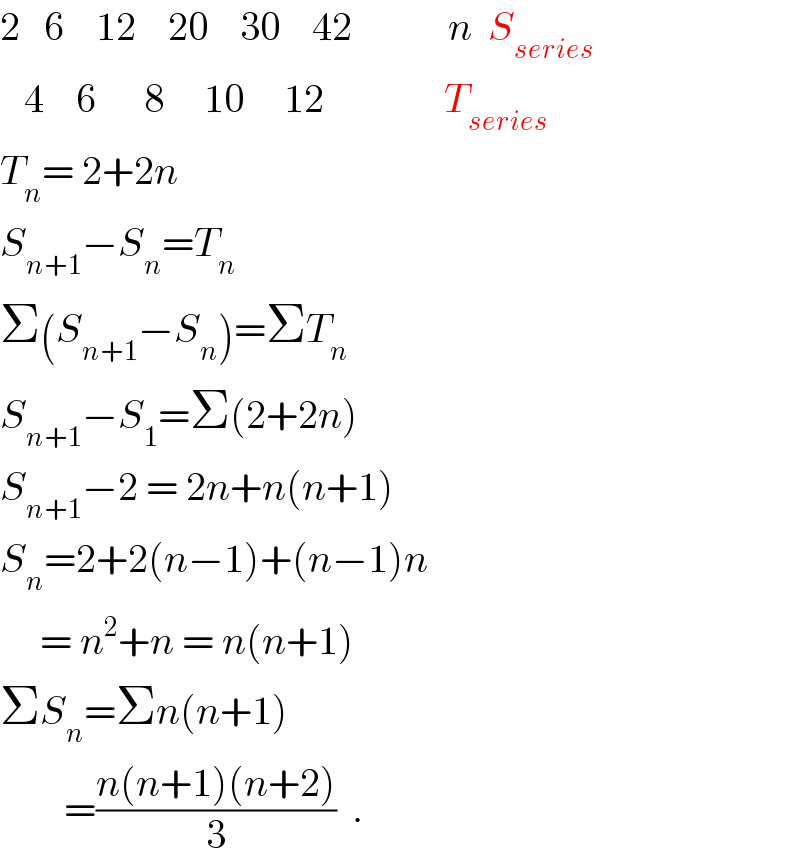
$$\mathrm{2}\:\:\:\mathrm{6}\:\:\:\:\mathrm{12}\:\:\:\:\mathrm{20}\:\:\:\:\mathrm{30}\:\:\:\:\mathrm{42}\:\:\:\:\:\:\:\:\:\:\:\:{n}\:\:{S}_{{series}} \\ $$$$\:\:\:\mathrm{4}\:\:\:\:\mathrm{6}\:\:\:\:\:\:\mathrm{8}\:\:\:\:\:\mathrm{10}\:\:\:\:\:\mathrm{12}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{T}_{{series}} \:\:\: \\ $$$${T}_{{n}} =\:\mathrm{2}+\mathrm{2}{n} \\ $$$${S}_{{n}+\mathrm{1}} −{S}_{{n}} ={T}_{{n}} \\ $$$$\Sigma\left({S}_{{n}+\mathrm{1}} −{S}_{{n}} \right)=\Sigma{T}_{{n}} \\ $$$${S}_{{n}+\mathrm{1}} −{S}_{\mathrm{1}} =\Sigma\left(\mathrm{2}+\mathrm{2}{n}\right) \\ $$$${S}_{{n}+\mathrm{1}} −\mathrm{2}\:=\:\mathrm{2}{n}+{n}\left({n}+\mathrm{1}\right) \\ $$$${S}_{{n}} =\mathrm{2}+\mathrm{2}\left({n}−\mathrm{1}\right)+\left({n}−\mathrm{1}\right){n} \\ $$$$\:\:\:\:\:=\:{n}^{\mathrm{2}} +{n}\:=\:{n}\left({n}+\mathrm{1}\right) \\ $$$$\Sigma{S}_{{n}} =\Sigma{n}\left({n}+\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:=\frac{{n}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}{\mathrm{3}}\:\:. \\ $$
Commented by kunal1234523 last updated on 17/Jun/18

$$\mathrm{thanks}\:\mathrm{a}\:\mathrm{lot} \\ $$
