Question Number 157829 by Fikret last updated on 28/Oct/21
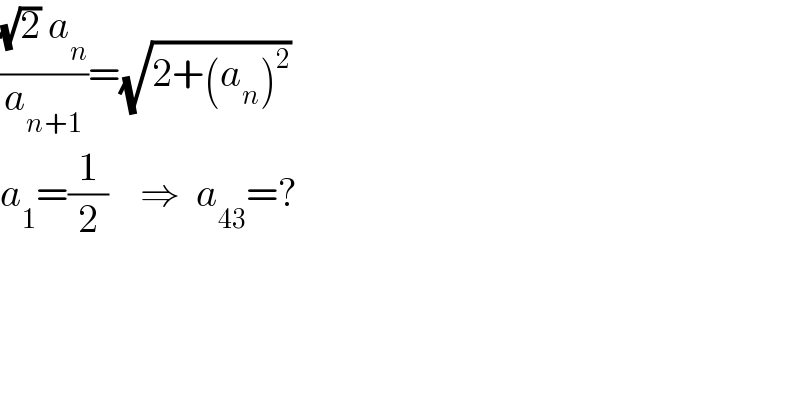
$$\frac{\sqrt{\mathrm{2}}\:{a}_{{n}} }{{a}_{{n}+\mathrm{1}} }=\sqrt{\mathrm{2}+\left({a}_{{n}} \right)^{\mathrm{2}} }\:\:\:\:\: \\ $$$${a}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\:\Rightarrow\:\:{a}_{\mathrm{43}} =? \\ $$
Answered by qaz last updated on 28/Oct/21
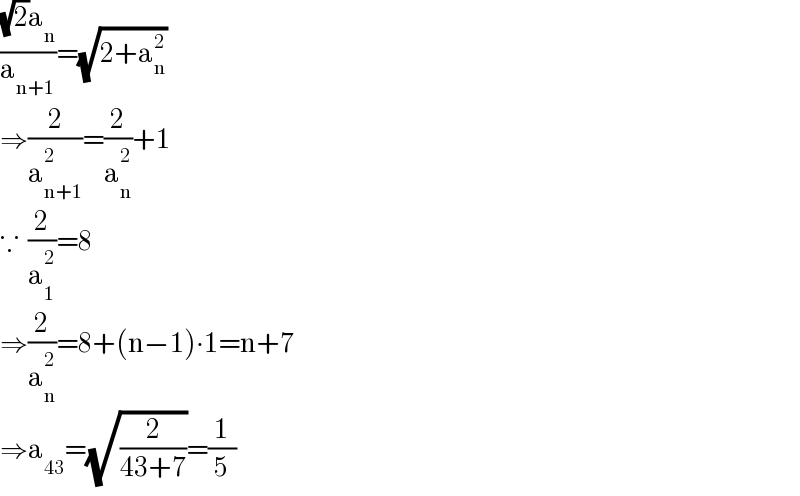
$$\frac{\sqrt{\mathrm{2}}\mathrm{a}_{\mathrm{n}} }{\mathrm{a}_{\mathrm{n}+\mathrm{1}} }=\sqrt{\mathrm{2}+\mathrm{a}_{\mathrm{n}} ^{\mathrm{2}} } \\ $$$$\Rightarrow\frac{\mathrm{2}}{\mathrm{a}_{\mathrm{n}+\mathrm{1}} ^{\mathrm{2}} }=\frac{\mathrm{2}}{\mathrm{a}_{\mathrm{n}} ^{\mathrm{2}} }+\mathrm{1} \\ $$$$\because\:\:\frac{\mathrm{2}}{\mathrm{a}_{\mathrm{1}} ^{\mathrm{2}} }=\mathrm{8} \\ $$$$\Rightarrow\frac{\mathrm{2}}{\mathrm{a}_{\mathrm{n}} ^{\mathrm{2}} }=\mathrm{8}+\left(\mathrm{n}−\mathrm{1}\right)\centerdot\mathrm{1}=\mathrm{n}+\mathrm{7} \\ $$$$\Rightarrow\mathrm{a}_{\mathrm{43}} =\sqrt{\frac{\mathrm{2}}{\mathrm{43}+\mathrm{7}}}=\frac{\mathrm{1}}{\mathrm{5}} \\ $$
Commented by Rasheed.Sindhi last updated on 29/Oct/21

$${Qaz}\:{sir}\:{How}\:{do}\:{you}\:{conclude}?: \\ $$$$\:\:\frac{\mathrm{2}}{\mathrm{a}_{\mathrm{n}} ^{\mathrm{2}} }=\mathrm{8}+\left(\mathrm{n}−\mathrm{1}\right)\centerdot\mathrm{1}=\mathrm{n}+\mathrm{7} \\ $$$$ \\ $$
Commented by mr W last updated on 29/Oct/21

$${let}\:{b}_{{n}} =\frac{\mathrm{2}}{{a}_{{n}} ^{\mathrm{2}} } \\ $$$${b}_{{n}+\mathrm{1}} ={b}_{{n}} +\mathrm{1}\:\:\:\Rightarrow\:{A}.{P}.\:{with}\:{c}.{d}.=\mathrm{1} \\ $$$$\Rightarrow{b}_{{n}} ={b}_{\mathrm{1}} +\left({n}−\mathrm{1}\right)×\mathrm{1} \\ $$$${b}_{\mathrm{1}} =\frac{\mathrm{2}}{{a}_{\mathrm{1}} ^{\mathrm{2}} }=\frac{\mathrm{2}}{\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }=\mathrm{8} \\ $$$$\Rightarrow{b}_{{n}} =\frac{\mathrm{2}}{{a}_{{n}} ^{\mathrm{2}} }=\mathrm{8}+{n}−\mathrm{1}={n}+\mathrm{7} \\ $$$$\Rightarrow{a}_{{n}} =\sqrt{\frac{\mathrm{2}}{{n}+\mathrm{7}}} \\ $$
Commented by Rasheed.Sindhi last updated on 29/Oct/21

$$\mathcal{T}{han}\mathcal{X}\:\:\mathcal{S}{ir}! \\ $$
