Question Number 149121 by mathdanisur last updated on 03/Aug/21
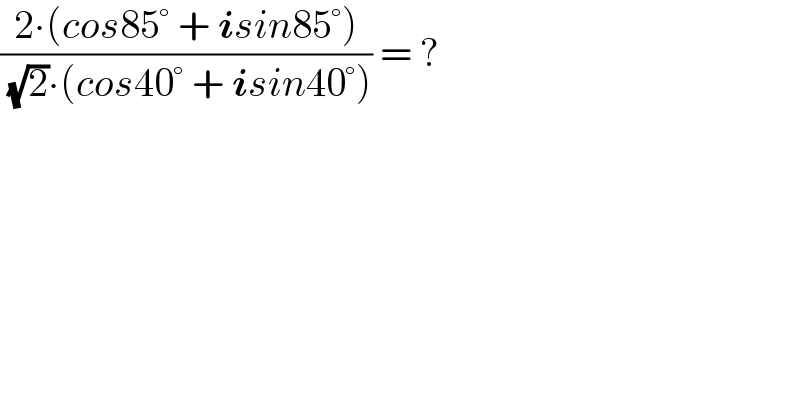
$$\frac{\mathrm{2}\centerdot\left({cos}\mathrm{85}°\:+\:\boldsymbol{{i}}{sin}\mathrm{85}°\right)}{\:\sqrt{\mathrm{2}}\centerdot\left({cos}\mathrm{40}°\:+\:\boldsymbol{{i}}{sin}\mathrm{40}°\right)}\:=\:? \\ $$
Answered by bramlexs22 last updated on 03/Aug/21
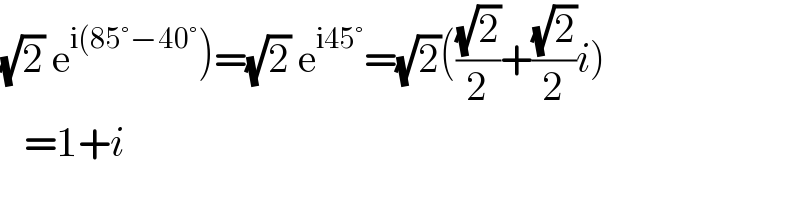
$$\left.\sqrt{\mathrm{2}}\:\mathrm{e}^{\mathrm{i}\left(\mathrm{85}°−\mathrm{40}°\right.} \right)=\sqrt{\mathrm{2}}\:\mathrm{e}^{\mathrm{i45}°} =\sqrt{\mathrm{2}}\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}{i}\right) \\ $$$$\:\:\:=\mathrm{1}+{i} \\ $$
Commented by mathdanisur last updated on 03/Aug/21

$${Ser},\:{Thank}\:{You} \\ $$
Answered by Ar Brandon last updated on 03/Aug/21
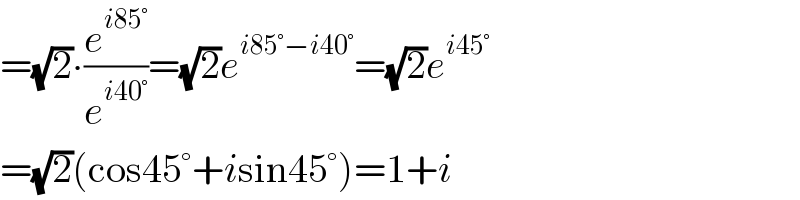
$$=\sqrt{\mathrm{2}}\centerdot\frac{{e}^{{i}\mathrm{85}°} }{{e}^{{i}\mathrm{40}°} }=\sqrt{\mathrm{2}}{e}^{{i}\mathrm{85}°−{i}\mathrm{40}°} =\sqrt{\mathrm{2}}{e}^{{i}\mathrm{45}°} \\ $$$$=\sqrt{\mathrm{2}}\left(\mathrm{cos45}°+{i}\mathrm{sin45}°\right)=\mathrm{1}+{i} \\ $$
Commented by mathdanisur last updated on 03/Aug/21

$${Ser},\:{Thank}\:{You} \\ $$
