Question Number 89205 by jagoll last updated on 16/Apr/20
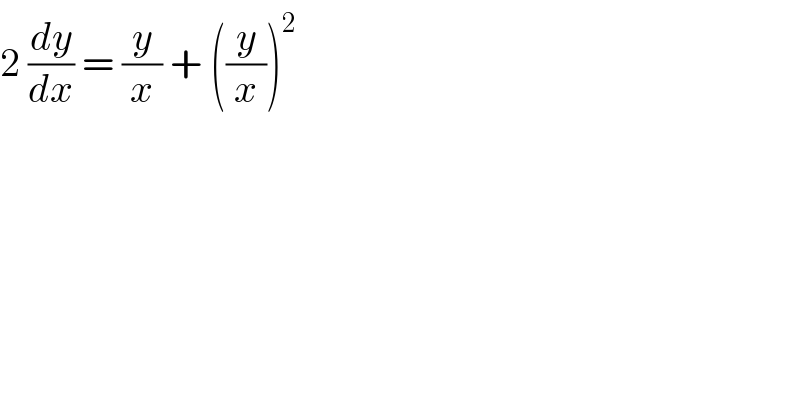
$$\mathrm{2}\:\frac{{dy}}{{dx}}\:=\:\frac{{y}}{{x}}\:+\:\left(\frac{{y}}{{x}}\right)^{\mathrm{2}} \\ $$
Commented by john santu last updated on 16/Apr/20
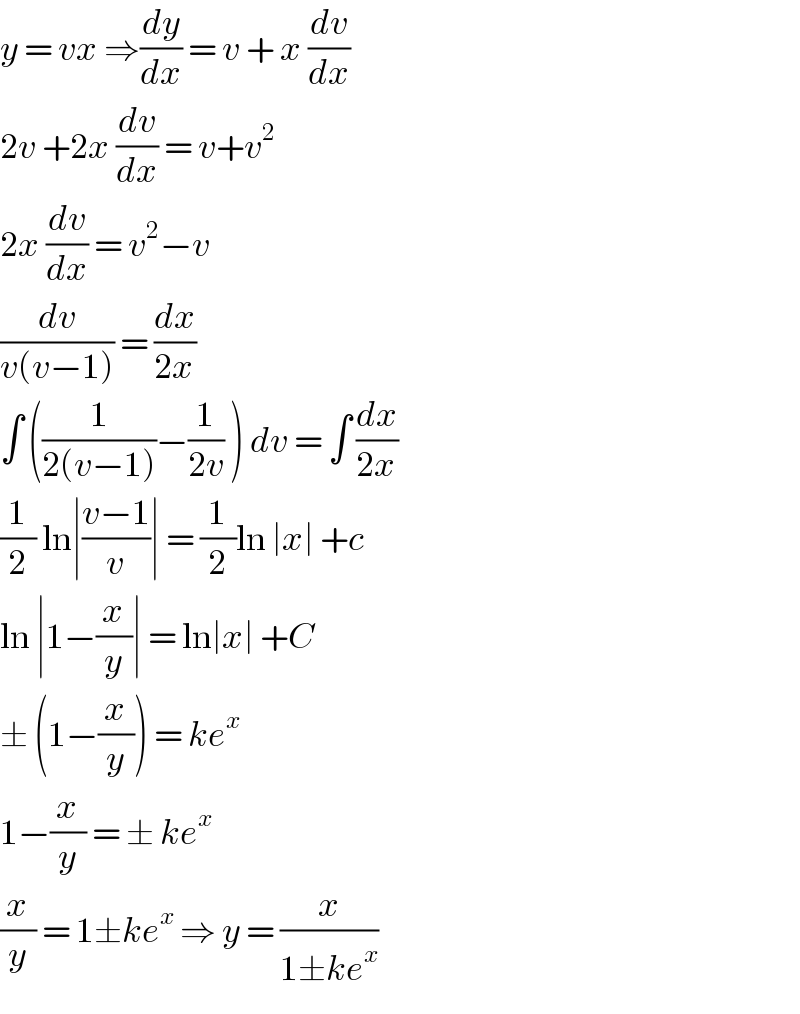
$${y}\:=\:{vx}\:\Rightarrow\frac{{dy}}{{dx}}\:=\:{v}\:+\:{x}\:\frac{{dv}}{{dx}} \\ $$$$\mathrm{2}{v}\:+\mathrm{2}{x}\:\frac{{dv}}{{dx}}\:=\:{v}+{v}^{\mathrm{2}} \\ $$$$\mathrm{2}{x}\:\frac{{dv}}{{dx}}\:=\:{v}^{\mathrm{2}} −{v} \\ $$$$\frac{{dv}}{{v}\left({v}−\mathrm{1}\right)}\:=\:\frac{{dx}}{\mathrm{2}{x}} \\ $$$$\int\:\left(\frac{\mathrm{1}}{\mathrm{2}\left({v}−\mathrm{1}\right)}−\frac{\mathrm{1}}{\mathrm{2}{v}}\:\right)\:{dv}\:=\:\int\:\frac{{dx}}{\mathrm{2}{x}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{ln}\mid\frac{{v}−\mathrm{1}}{{v}}\mid\:=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mid{x}\mid\:+{c} \\ $$$$\mathrm{ln}\:\mid\mathrm{1}−\frac{{x}}{{y}}\mid\:=\:\mathrm{ln}\mid{x}\mid\:+{C} \\ $$$$\pm\:\left(\mathrm{1}−\frac{{x}}{{y}}\right)\:=\:{ke}^{{x}} \: \\ $$$$\mathrm{1}−\frac{{x}}{{y}}\:=\:\pm\:{ke}^{{x}} \: \\ $$$$\frac{{x}}{{y}}\:=\:\mathrm{1}\pm{ke}^{{x}} \:\Rightarrow\:{y}\:=\:\frac{{x}}{\mathrm{1}\pm{ke}^{{x}} } \\ $$
Answered by 242242864 last updated on 16/Apr/20
![let u = (y/x) ⇒y=ux (dy/dx)=u+x(du/dx) 2[u+x(du/dx)]=u+u^2 2u+2x(du/dc) = u+u^2 2x(du/dx)=u^2 −u 2xdu=(u^2 −u)dx ((2du)/((u^2 −u)))=(dx/x) 2∫(du/((u^2 −u)))=∫(dx/x) consider (1/((u^2 −u))) to be change to partial fraction, (1/((u^2 −u)))= (1/((u+1)(u−1))) ⇒(1/((u+1)(u−1))) = (A/((u+1)))+(B/((u−1))) 1= A(u−1)+B(u+1) 1= Au−A+Bu+B 1=u(A+B)+B−A B−A=1.........(i) A+B=0..........(ii) ⇒A= −(1/2), B = (1/2) ⇒∫(1/((u^2 −1)))du = (1/2)∫(du/((u−1)))−(1/2)∫(du/((u+1))) = ∫(dx/x) (1/2)ln(u−1)−(1/2)ln(u+1)=lnx+C (1/2)ln[((u−1)/(u+1))]= lnx+C (1/2)ln[((y−x)/(y+x))] = lnx+C](https://www.tinkutara.com/question/Q89235.png)
$$\mathrm{let}\:\mathrm{u}\:=\:\frac{{y}}{{x}} \\ $$$$\Rightarrow{y}={ux} \\ $$$$\frac{\boldsymbol{{dy}}}{\boldsymbol{{dx}}}=\boldsymbol{{u}}+\boldsymbol{{x}}\frac{\boldsymbol{{du}}}{\boldsymbol{{dx}}} \\ $$$$\mathrm{2}\left[\boldsymbol{{u}}+\boldsymbol{{x}}\frac{\boldsymbol{{du}}}{\boldsymbol{{dx}}}\right]=\boldsymbol{{u}}+\boldsymbol{{u}}^{\mathrm{2}} \\ $$$$\mathrm{2}\boldsymbol{{u}}+\mathrm{2}\boldsymbol{{x}}\frac{\boldsymbol{{du}}}{\boldsymbol{{dc}}}\:=\:\boldsymbol{{u}}+\boldsymbol{{u}}^{\mathrm{2}} \\ $$$$\mathrm{2}\boldsymbol{{x}}\frac{\boldsymbol{{du}}}{\boldsymbol{{dx}}}=\boldsymbol{{u}}^{\mathrm{2}} −\boldsymbol{{u}} \\ $$$$\mathrm{2}\boldsymbol{{xdu}}=\left(\boldsymbol{{u}}^{\mathrm{2}} −\boldsymbol{{u}}\right)\boldsymbol{{dx}} \\ $$$$\frac{\mathrm{2}\boldsymbol{{du}}}{\left(\boldsymbol{{u}}^{\mathrm{2}} −\boldsymbol{{u}}\right)}=\frac{\boldsymbol{{dx}}}{\boldsymbol{{x}}} \\ $$$$\mathrm{2}\int\frac{\boldsymbol{{du}}}{\left(\boldsymbol{{u}}^{\mathrm{2}} −\boldsymbol{{u}}\right)}=\int\frac{\boldsymbol{{dx}}}{\boldsymbol{{x}}} \\ $$$$\boldsymbol{{consider}}\:\frac{\mathrm{1}}{\left(\boldsymbol{{u}}^{\mathrm{2}} −\boldsymbol{{u}}\right)}\:\boldsymbol{{to}}\:\boldsymbol{{be}}\:\boldsymbol{{change}}\:\boldsymbol{{to}}\:\boldsymbol{{partial}}\:\boldsymbol{{fraction}}, \\ $$$$\frac{\mathrm{1}}{\left(\boldsymbol{{u}}^{\mathrm{2}} −\boldsymbol{{u}}\right)}=\:\frac{\mathrm{1}}{\left(\boldsymbol{{u}}+\mathrm{1}\right)\left(\boldsymbol{{u}}−\mathrm{1}\right)} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\left(\boldsymbol{{u}}+\mathrm{1}\right)\left(\boldsymbol{{u}}−\mathrm{1}\right)}\:=\:\frac{{A}}{\left(\boldsymbol{{u}}+\mathrm{1}\right)}+\frac{{B}}{\left(\boldsymbol{{u}}−\mathrm{1}\right)} \\ $$$$\mathrm{1}=\:{A}\left(\boldsymbol{{u}}−\mathrm{1}\right)+{B}\left(\boldsymbol{{u}}+\mathrm{1}\right) \\ $$$$\mathrm{1}=\:{A}\boldsymbol{{u}}−{A}+{B}\boldsymbol{{u}}+{B} \\ $$$$\mathrm{1}=\boldsymbol{{u}}\left({A}+{B}\right)+{B}−{A} \\ $$$${B}−{A}=\mathrm{1}………\left({i}\right) \\ $$$${A}+{B}=\mathrm{0}……….\left({ii}\right) \\ $$$$\Rightarrow{A}=\:−\frac{\mathrm{1}}{\mathrm{2}},\:{B}\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\int\frac{\mathrm{1}}{\left(\boldsymbol{{u}}^{\mathrm{2}} −\mathrm{1}\right)}\boldsymbol{{du}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\boldsymbol{{du}}}{\left(\boldsymbol{{u}}−\mathrm{1}\right)}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\boldsymbol{{du}}}{\left(\boldsymbol{{u}}+\mathrm{1}\right)}\:=\:\int\frac{\boldsymbol{{dx}}}{\boldsymbol{{x}}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{{ln}}\left(\boldsymbol{{u}}−\mathrm{1}\right)−\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{{ln}}\left(\boldsymbol{{u}}+\mathrm{1}\right)=\boldsymbol{{lnx}}+{C} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{{ln}}\left[\frac{\boldsymbol{{u}}−\mathrm{1}}{\boldsymbol{{u}}+\mathrm{1}}\right]=\:\boldsymbol{{lnx}}+{C} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{{ln}}\left[\frac{\boldsymbol{{y}}−\boldsymbol{{x}}}{\boldsymbol{{y}}+\boldsymbol{{x}}}\right]\:=\:\boldsymbol{{lnx}}+{C} \\ $$$$ \\ $$
