Menu Close

2-lines-through-the-point-A-5-1-are-tangent-to-the-circle-x-2-y-2-4x-6y-4-0-Find-the-equation-of-these-2-lines-

Tinku Tara 0 Comments
Pin




Question Number 31249 by Joel578 last updated on 04/Mar/18
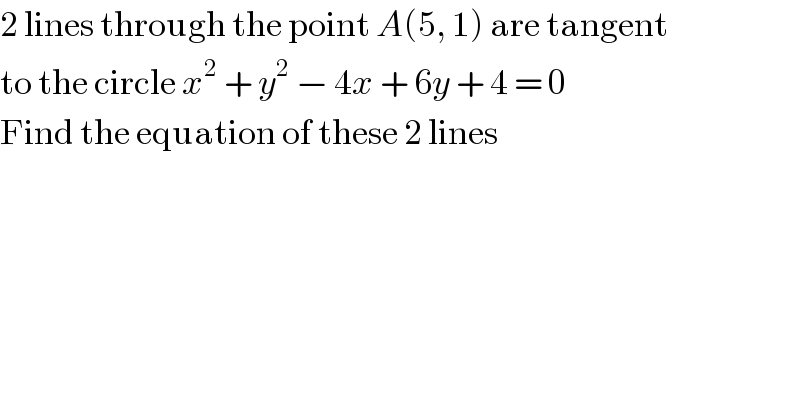
2 lines through the point A(5, 1) are tangent to the circle x^2 + y^2 − 4x + 6y + 4 = 0 Find the equation of these 2 lines
$$\mathrm{2}\:\mathrm{lines}\:\mathrm{through}\:\mathrm{the}\:\mathrm{point}\:{A}\left(\mathrm{5},\:\mathrm{1}\right)\:\mathrm{are}\:\mathrm{tangent} \\ $$$$\mathrm{to}\:\mathrm{the}\:\mathrm{circle}\:{x}^{\mathrm{2}} \:+\:{y}^{\mathrm{2}} \:−\:\mathrm{4}{x}\:+\:\mathrm{6}{y}\:+\:\mathrm{4}\:=\:\mathrm{0} \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{these}\:\mathrm{2}\:\mathrm{lines} \\ $$
Commented by Joel578 last updated on 04/Mar/18
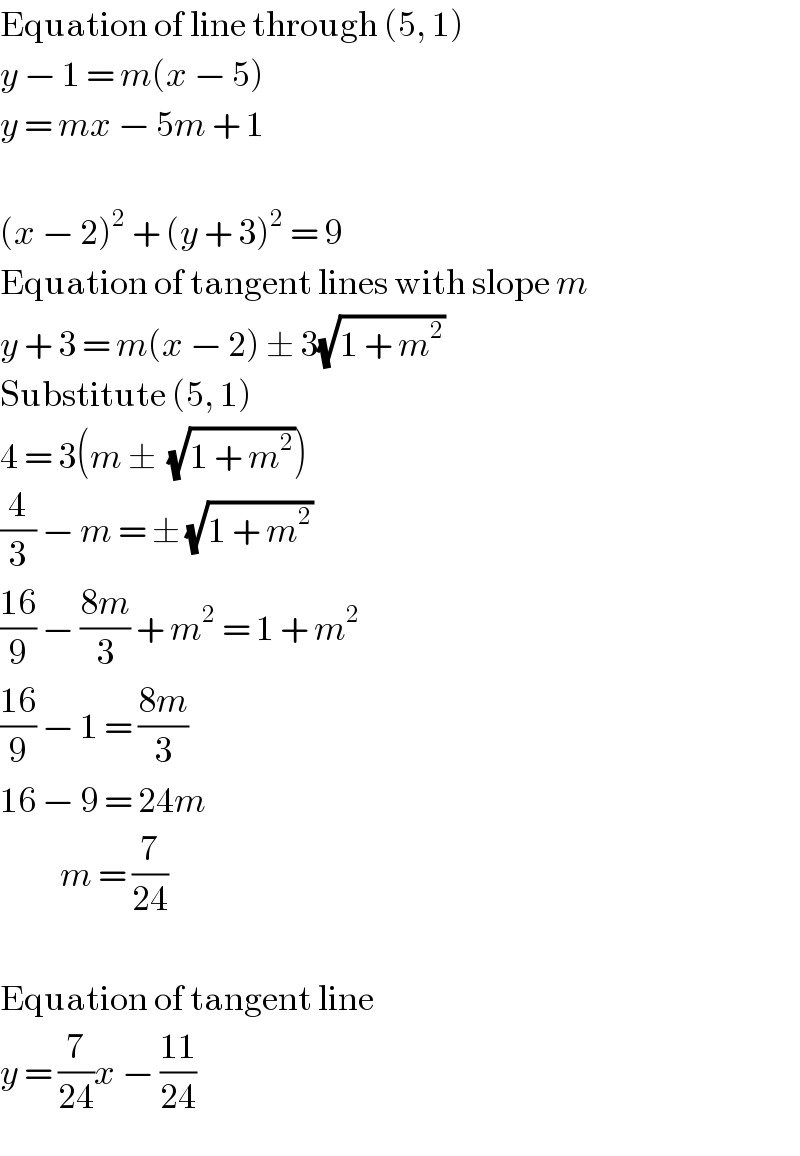
Equation of line through (5, 1) y − 1 = m(x − 5) y = mx − 5m + 1 (x − 2)^2 + (y + 3)^2 = 9 Equation of tangent lines with slope m y + 3 = m(x − 2) ± 3(√(1 + m^2 )) Substitute (5, 1) 4 = 3(m ± (√(1 + m^2 ))) (4/3) − m = ± (√(1 + m^2 )) ((16)/9) − ((8m)/3) + m^2 = 1 + m^2 ((16)/9) − 1 = ((8m)/3) 16 − 9 = 24m m = (7/(24)) Equation of tangent line y = (7/(24))x − ((11)/(24))
$$\mathrm{Equation}\:\mathrm{of}\:\mathrm{line}\:\mathrm{through}\:\left(\mathrm{5},\:\mathrm{1}\right) \\ $$$${y}\:−\:\mathrm{1}\:=\:{m}\left({x}\:−\:\mathrm{5}\right) \\ $$$${y}\:=\:{mx}\:−\:\mathrm{5}{m}\:+\:\mathrm{1} \\ $$$$ \\ $$$$\left({x}\:−\:\mathrm{2}\right)^{\mathrm{2}} \:+\:\left({y}\:+\:\mathrm{3}\right)^{\mathrm{2}} \:=\:\mathrm{9} \\ $$$$\mathrm{Equation}\:\mathrm{of}\:\mathrm{tangent}\:\mathrm{lines}\:\mathrm{with}\:\mathrm{slope}\:{m} \\ $$$${y}\:+\:\mathrm{3}\:=\:{m}\left({x}\:−\:\mathrm{2}\right)\:\pm\:\mathrm{3}\sqrt{\mathrm{1}\:+\:{m}^{\mathrm{2}} } \\ $$$$\mathrm{Substitute}\:\left(\mathrm{5},\:\mathrm{1}\right) \\ $$$$\mathrm{4}\:=\:\mathrm{3}\left({m}\:\pm\:\:\sqrt{\mathrm{1}\:+\:{m}^{\mathrm{2}} }\right) \\ $$$$\frac{\mathrm{4}}{\mathrm{3}}\:−\:{m}\:=\:\pm\:\sqrt{\mathrm{1}\:+\:{m}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{16}}{\mathrm{9}}\:−\:\frac{\mathrm{8}{m}}{\mathrm{3}}\:+\:{m}^{\mathrm{2}} \:=\:\mathrm{1}\:+\:{m}^{\mathrm{2}} \\ $$$$\frac{\mathrm{16}}{\mathrm{9}}\:−\:\mathrm{1}\:=\:\frac{\mathrm{8}{m}}{\mathrm{3}} \\ $$$$\mathrm{16}\:−\:\mathrm{9}\:=\:\mathrm{24}{m} \\ $$$$\:\:\:\:\:\:\:\:\:\:{m}\:=\:\frac{\mathrm{7}}{\mathrm{24}} \\ $$$$ \\ $$$$\mathrm{Equation}\:\mathrm{of}\:\mathrm{tangent}\:\mathrm{line} \\ $$$${y}\:=\:\frac{\mathrm{7}}{\mathrm{24}}{x}\:−\:\frac{\mathrm{11}}{\mathrm{24}} \\ $$
Commented by Joel578 last updated on 04/Mar/18
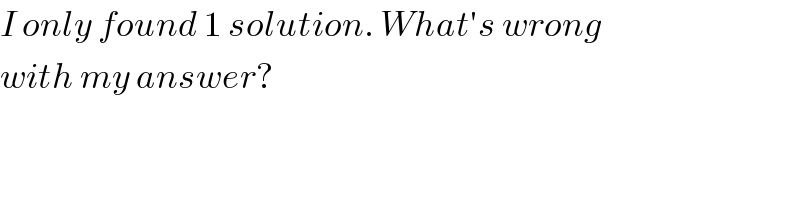
I only found 1 solution. What′s wrong with my answer?
$${I}\:{only}\:{found}\:\mathrm{1}\:{solution}.\:{What}'{s}\:{wrong} \\ $$$${with}\:{my}\:{answer}? \\ $$
Commented by ajfour last updated on 04/Mar/18
Also m=∞ so another tangent is x−5 = 0 .
$${Also}\:\:{m}=\infty \\ $$$${so}\:\:{another}\:{tangent}\:{is}\:\: \\ $$$${x}−\mathrm{5}\:=\:\mathrm{0}\:\:. \\ $$
Commented by Joel578 last updated on 05/Mar/18
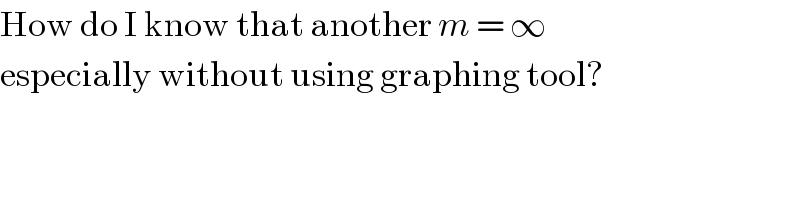
How do I know that another m = ∞ especially without using graphing tool?
$$\mathrm{How}\:\mathrm{do}\:\mathrm{I}\:\mathrm{know}\:\mathrm{that}\:\mathrm{another}\:{m}\:=\:\infty \\ $$$$\mathrm{especially}\:\mathrm{without}\:\mathrm{using}\:\mathrm{graphing}\:\mathrm{tool}? \\ $$
Commented by ajfour last updated on 05/Mar/18
when you cancel term of m^2 , you should realise that m=±∞ is of course the roots. For example m^2 =(m−2)^2 ⇒ m^2 =m^2 −4m+4 this eq. has roots m=±∞ and m=1 .
$${when}\:{you}\:{cancel}\:{term}\:{of}\:\:{m}^{\mathrm{2}} \:, \\ $$$${you}\:{should}\:{realise}\:{that}\:{m}=\pm\infty\:{is} \\ $$$${of}\:{course}\:{the}\:{roots}.\:{For}\:{example} \\ $$$${m}^{\mathrm{2}} =\left({m}−\mathrm{2}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\:{m}^{\mathrm{2}} ={m}^{\mathrm{2}} −\mathrm{4}{m}+\mathrm{4} \\ $$$${this}\:{eq}.\:{has}\:\:{roots} \\ $$$${m}=\pm\infty\:\:{and}\:\:{m}=\mathrm{1}\:\:. \\ $$
Commented by Joel578 last updated on 05/Mar/18
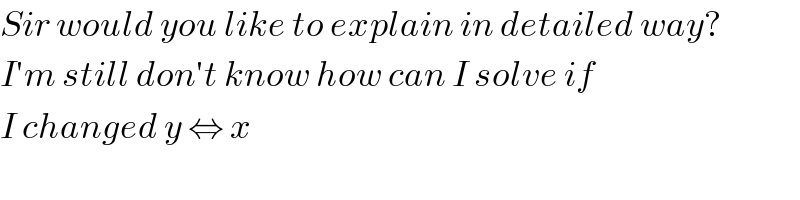
Sir would you like to explain in detailed way? I′m still don′t know how can I solve if I changed y ⇔ x
$${Sir}\:{would}\:{you}\:{like}\:{to}\:{explain}\:{in}\:{detailed}\:{way}? \\ $$$${I}'{m}\:{still}\:{don}'{t}\:{know}\:{how}\:{can}\:{I}\:{solve}\:{if} \\ $$$${I}\:{changed}\:{y}\:\Leftrightarrow\:{x} \\ $$
Commented by Joel578 last updated on 05/Mar/18
Okay. Thank you very much
$${Okay}.\:{Thank}\:{you}\:{very}\:{much} \\ $$
Commented by MJS last updated on 05/Mar/18
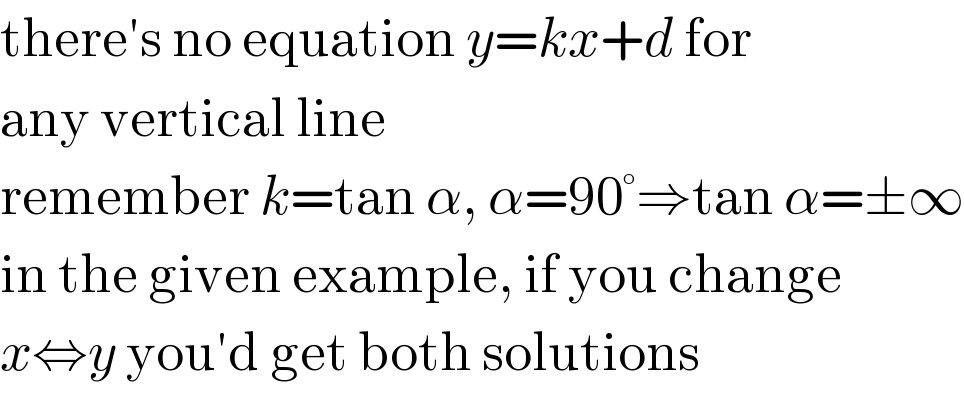
there′s no equation y=kx+d for any vertical line remember k=tan α, α=90°⇒tan α=±∞ in the given example, if you change x⇔y you′d get both solutions
$$\mathrm{there}'\mathrm{s}\:\mathrm{no}\:\mathrm{equation}\:{y}={kx}+{d}\:\mathrm{for} \\ $$$$\mathrm{any}\:\mathrm{vertical}\:\mathrm{line} \\ $$$$\mathrm{remember}\:{k}=\mathrm{tan}\:\alpha,\:\alpha=\mathrm{90}°\Rightarrow\mathrm{tan}\:\alpha=\pm\infty \\ $$$$\mathrm{in}\:\mathrm{the}\:\mathrm{given}\:\mathrm{example},\:\mathrm{if}\:\mathrm{you}\:\mathrm{change} \\ $$$${x}\Leftrightarrow{y}\:\mathrm{you}'\mathrm{d}\:\mathrm{get}\:\mathrm{both}\:\mathrm{solutions} \\ $$
Commented by MJS last updated on 05/Mar/18
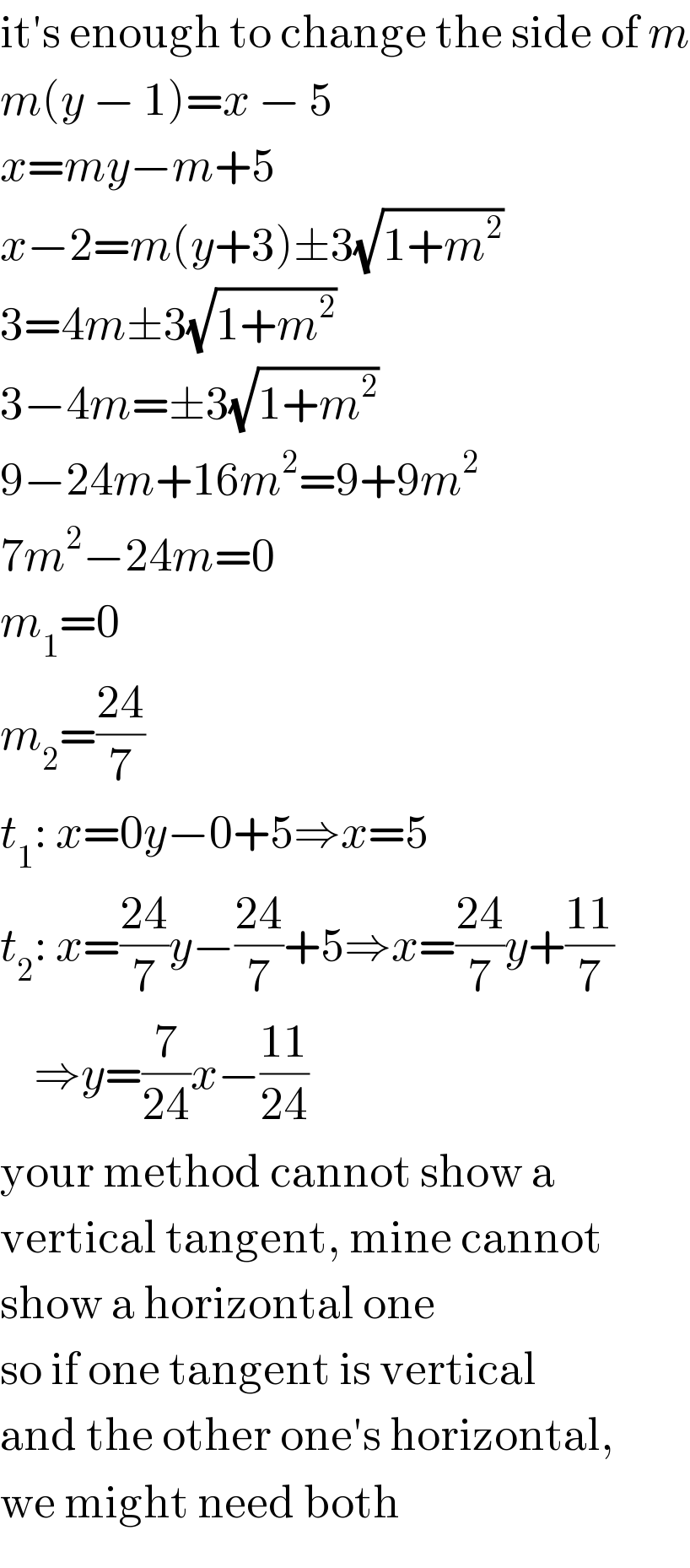
it′s enough to change the side of m m(y − 1)=x − 5 x=my−m+5 x−2=m(y+3)±3(√(1+m^2 )) 3=4m±3(√(1+m^2 )) 3−4m=±3(√(1+m^2 )) 9−24m+16m^2 =9+9m^2 7m^2 −24m=0 m_1 =0 m_2 =((24)/7) t_1 : x=0y−0+5⇒x=5 t_2 : x=((24)/7)y−((24)/7)+5⇒x=((24)/7)y+((11)/7) ⇒y=(7/(24))x−((11)/(24)) your method cannot show a vertical tangent, mine cannot show a horizontal one so if one tangent is vertical and the other one′s horizontal, we might need both
$$\mathrm{it}'\mathrm{s}\:\mathrm{enough}\:\mathrm{to}\:\mathrm{change}\:\mathrm{the}\:\mathrm{side}\:\mathrm{of}\:{m} \\ $$$${m}\left({y}\:−\:\mathrm{1}\right)={x}\:−\:\mathrm{5} \\ $$$${x}={my}−{m}+\mathrm{5} \\ $$$${x}−\mathrm{2}={m}\left({y}+\mathrm{3}\right)\pm\mathrm{3}\sqrt{\mathrm{1}+{m}^{\mathrm{2}} } \\ $$$$\mathrm{3}=\mathrm{4}{m}\pm\mathrm{3}\sqrt{\mathrm{1}+{m}^{\mathrm{2}} } \\ $$$$\mathrm{3}−\mathrm{4}{m}=\pm\mathrm{3}\sqrt{\mathrm{1}+{m}^{\mathrm{2}} } \\ $$$$\mathrm{9}−\mathrm{24}{m}+\mathrm{16}{m}^{\mathrm{2}} =\mathrm{9}+\mathrm{9}{m}^{\mathrm{2}} \\ $$$$\mathrm{7}{m}^{\mathrm{2}} −\mathrm{24}{m}=\mathrm{0} \\ $$$${m}_{\mathrm{1}} =\mathrm{0} \\ $$$${m}_{\mathrm{2}} =\frac{\mathrm{24}}{\mathrm{7}} \\ $$$${t}_{\mathrm{1}} :\:{x}=\mathrm{0}{y}−\mathrm{0}+\mathrm{5}\Rightarrow{x}=\mathrm{5} \\ $$$${t}_{\mathrm{2}} :\:{x}=\frac{\mathrm{24}}{\mathrm{7}}{y}−\frac{\mathrm{24}}{\mathrm{7}}+\mathrm{5}\Rightarrow{x}=\frac{\mathrm{24}}{\mathrm{7}}{y}+\frac{\mathrm{11}}{\mathrm{7}} \\ $$$$\:\:\:\:\Rightarrow{y}=\frac{\mathrm{7}}{\mathrm{24}}{x}−\frac{\mathrm{11}}{\mathrm{24}} \\ $$$$\mathrm{your}\:\mathrm{method}\:\mathrm{cannot}\:\mathrm{show}\:\mathrm{a} \\ $$$$\mathrm{vertical}\:\mathrm{tangent},\:\mathrm{mine}\:\mathrm{cannot} \\ $$$$\mathrm{show}\:\mathrm{a}\:\mathrm{horizontal}\:\mathrm{one} \\ $$$$\mathrm{so}\:\mathrm{if}\:\mathrm{one}\:\mathrm{tangent}\:\mathrm{is}\:\mathrm{vertical} \\ $$$$\mathrm{and}\:\mathrm{the}\:\mathrm{other}\:\mathrm{one}'\mathrm{s}\:\mathrm{horizontal}, \\ $$$$\mathrm{we}\:\mathrm{might}\:\mathrm{need}\:\mathrm{both} \\ $$
Commented by Joel578 last updated on 06/Mar/18
Okay, thank you for the explanation
$${Okay},\:{thank}\:{you}\:{for}\:{the}\:{explanation} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *