Question Number 80780 by naka3546 last updated on 06/Feb/20
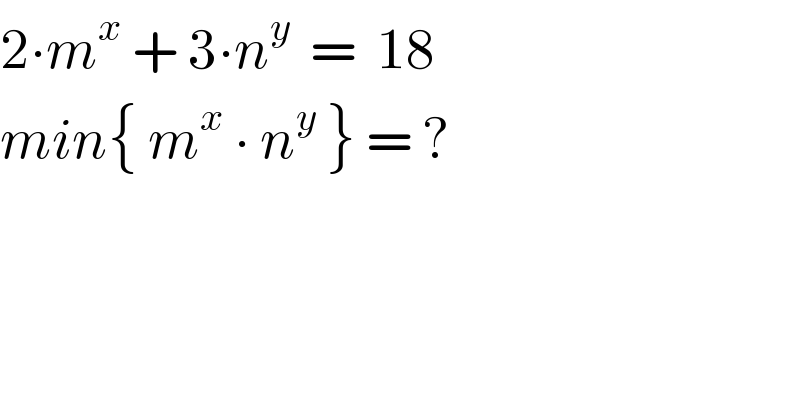
$$\mathrm{2}\centerdot{m}^{{x}} \:+\:\mathrm{3}\centerdot{n}^{{y}} \:\:=\:\:\mathrm{18} \\ $$$${min}\left\{\:{m}^{{x}} \:\centerdot\:{n}^{{y}} \:\right\}\:=\:? \\ $$
Commented by naka3546 last updated on 06/Feb/20

$${m},\:{n},\:{x},\:{y}\:\in\:\mathbb{N} \\ $$
Answered by key of knowledge last updated on 06/Feb/20
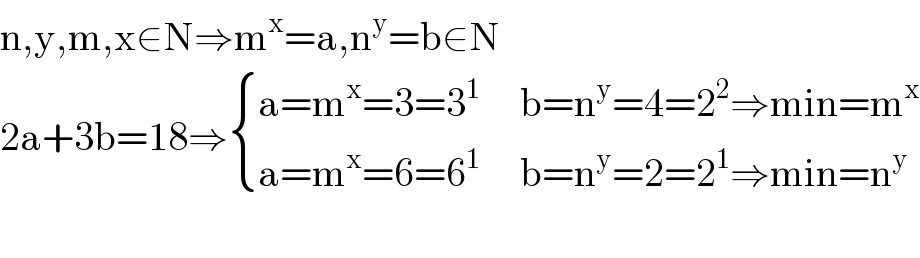
$$\mathrm{n},\mathrm{y},\mathrm{m},\mathrm{x}\in\mathrm{N}\Rightarrow\mathrm{m}^{\mathrm{x}} =\mathrm{a},\mathrm{n}^{\mathrm{y}} =\mathrm{b}\in\mathrm{N} \\ $$$$\mathrm{2a}+\mathrm{3b}=\mathrm{18}\Rightarrow\begin{cases}{\mathrm{a}=\mathrm{m}^{\mathrm{x}} =\mathrm{3}=\mathrm{3}^{\mathrm{1}} \:\:\:\:\:\mathrm{b}=\mathrm{n}^{\mathrm{y}} =\mathrm{4}=\mathrm{2}^{\mathrm{2}} \Rightarrow\mathrm{min}=\mathrm{m}^{\mathrm{x}} }\\{\mathrm{a}=\mathrm{m}^{\mathrm{x}} =\mathrm{6}=\mathrm{6}^{\mathrm{1}} \:\:\:\:\:\mathrm{b}=\mathrm{n}^{\mathrm{y}} =\mathrm{2}=\mathrm{2}^{\mathrm{1}} \Rightarrow\mathrm{min}=\mathrm{n}^{\mathrm{y}} }\end{cases} \\ $$$$ \\ $$
