2-opposite-vertices-of-a-square-are-5-4-and-1-6-Find-coordinates-of-remaining-two-vertices-

Question Number 50625 by rahul 19 last updated on 18/Dec/18

2 o p p o s i t e v e r t i c e s o f a s q u a r e a r e

(5, 4) a n d (1, - 6) . F i n d c o o r d i n a t e s

o f r e m a i n i n g t w o v e r t i c e s ?

Commented by $@ty@m last updated on 18/Dec/18

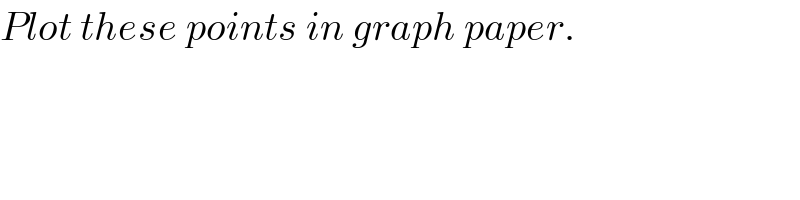
P l o t t h e s e p o i n t s i n g r a p h p a p e r .

Commented by rahul 19 last updated on 18/Dec/18

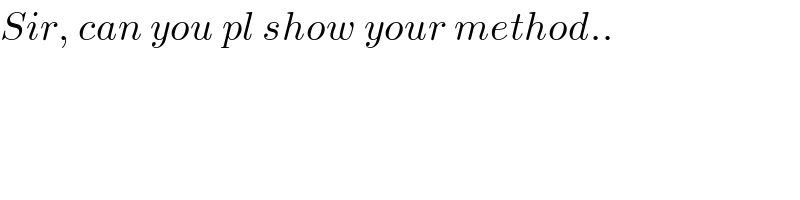
S i r, c a n y o u p l s h o w y o u r m e t h o d . .

Answered by ajfour last updated on 18/Dec/18

c e n t e r \equiv (3, - 1)

\frac{1}{2} \times d i a g o n a l = \sqrt{29}

s l o p e m = \frac{5}{2}

s l o p e o f C D = - \frac{2}{5}

x_{C} = 3 + \sqrt{29} (\frac{- 5}{\sqrt{29}}) = - 2

y_{C} = - 1 + \sqrt{29} (\frac{2}{\sqrt{29}}) = 1

x_{D} = 3 - \sqrt{29} (\frac{- 5}{29}) = 8

y_{D} = - 1 - \sqrt{29} (\frac{2}{\sqrt{29}}) = - 3

C \equiv (- 2, 1)

D \equiv (8, - 3) .

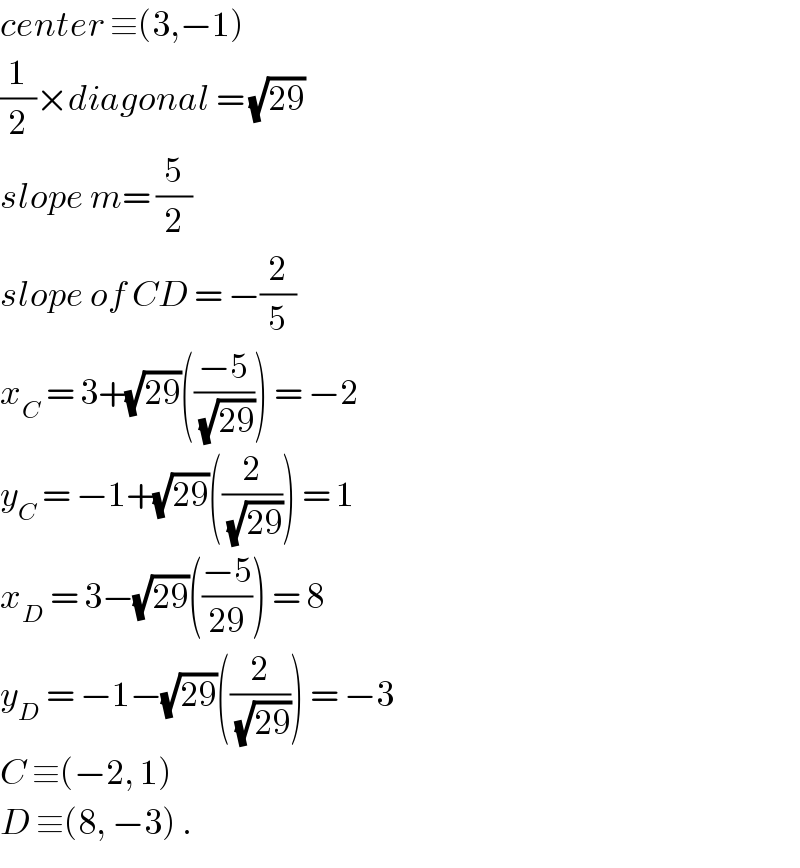
Commented by rahul 19 last updated on 18/Dec/18

thanks sir!��