Question Number 36475 by Rio Mike last updated on 02/Jun/18

$$\:\mathrm{2}\:{regtangle}\:{A}\:{and}\:{B}\:{given}\:{that} \\ $$$${the}\:{legnth}\:{of}\:{A}\:{is}\:{three}\:{times}\:{the} \\ $$$${legnth}\:{of}\:{B},{and}\:{the}\:{Perimeter}\:{of} \\ $$$${A}\:{is}\:\mathrm{102}{cm}.\:{If}\:{the}\:{Area}\:{of}\:{B}\:{is}\: \\ $$$${same}\:{as}\:\mathrm{2}\:{times}\:{the}\:{Area}\:{of}\:{a}\:{Trapezium} \\ $$$${with}\:\:\mathrm{2}\:{parrallel}\:{sides}\:\mathrm{5}{cm}\:{and}\:\mathrm{4}{cm} \\ $$$${with}\:{hieght}\:\mathrm{6}{cm}.\:{find}\:{the}\:{lengths} \\ $$$${and}\:{widths}\:{of}\:{A}\:{and}\:{B}. \\ $$
Commented by math1967 last updated on 02/Jun/18
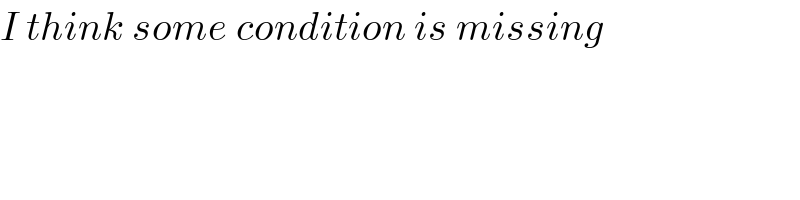
$${I}\:{think}\:{some}\:{condition}\:{is}\:{missing} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 03/Jun/18

$${rectangle}\:{A}\:{area}={l}_{{A}} ×{b}_{{A}} \\ $$$${recangle}\:{B}\:{area}={l}_{{B}} ×{b}_{{B}} \\ $$$${given}\:{l}_{{A}} =\mathrm{3}{l}_{{B}} \\ $$$${perimeter}\:{of}\:{A}=\mathrm{2}\left({l}_{{A}} +{b}_{{A}} \right)=\mathrm{102} \\ $$$${l}_{{A}} +{b}_{{A}} =\mathrm{51} \\ $$$$\mathrm{3}{l}_{{B}} +{b}_{{A}} =\mathrm{51} \\ $$$${l}_{{B}} ×{b}_{{B}} =\mathrm{2}×\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{5}+\mathrm{4}\right)×\mathrm{6} \\ $$$${l}_{{B}} ×{b}_{{B}} =\mathrm{54} \\ $$$$\mathrm{3}{l}_{{B}} +{b}_{{A}} =\mathrm{51} \\ $$$${so}\:{three}\:{unknown}\:\left({l}_{{B}} ,{b}_{{B}\:} {and}\:{b}_{{A}} \right) \\ $$$${two}\:{eqution}…{so}\:{data}\:{insufficiet} \\ $$
