Question Number 128329 by bramlexs22 last updated on 06/Jan/21
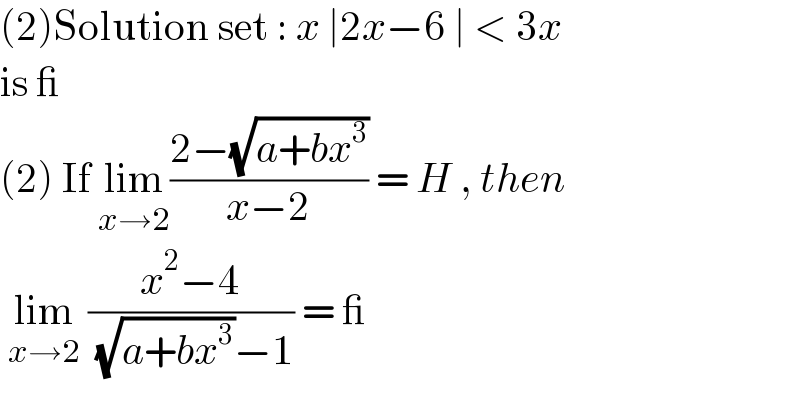
$$\left(\mathrm{2}\right)\mathrm{Solution}\:\mathrm{set}\::\:{x}\:\mid\mathrm{2}{x}−\mathrm{6}\:\mid\:<\:\mathrm{3}{x}\: \\ $$$$\mathrm{is}\:\_ \\ $$$$\left(\mathrm{2}\right)\:\mathrm{If}\:\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\frac{\mathrm{2}−\sqrt{{a}+{bx}^{\mathrm{3}} }}{{x}−\mathrm{2}}\:=\:{H}\:,\:{then} \\ $$$$\:\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{2}} −\mathrm{4}}{\:\sqrt{{a}+{bx}^{\mathrm{3}} }−\mathrm{1}}\:=\:\_ \\ $$
Answered by liberty last updated on 06/Jan/21
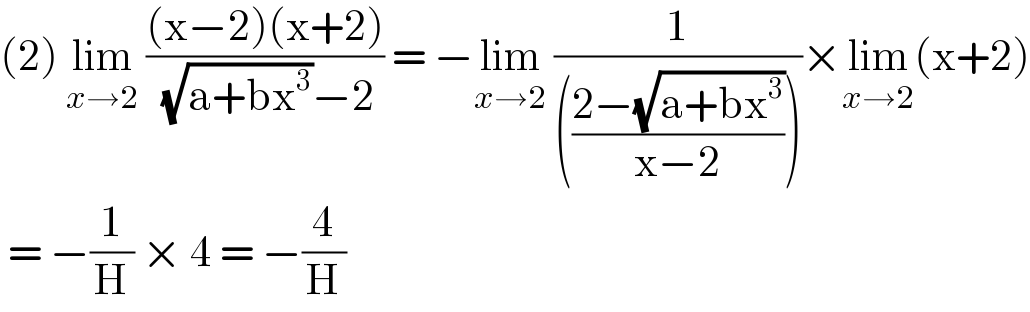
$$\left(\mathrm{2}\right)\:\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{\left(\mathrm{x}−\mathrm{2}\right)\left(\mathrm{x}+\mathrm{2}\right)}{\:\sqrt{\mathrm{a}+\mathrm{bx}^{\mathrm{3}} }−\mathrm{2}}\:=\:−\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\left(\frac{\mathrm{2}−\sqrt{\mathrm{a}+\mathrm{bx}^{\mathrm{3}} }}{\mathrm{x}−\mathrm{2}}\right)}×\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\left(\mathrm{x}+\mathrm{2}\right) \\ $$$$\:=\:−\frac{\mathrm{1}}{\mathrm{H}}\:×\:\mathrm{4}\:=\:−\frac{\mathrm{4}}{\mathrm{H}} \\ $$
Commented by bramlexs22 last updated on 06/Jan/21

$${creative} \\ $$
Answered by liberty last updated on 06/Jan/21
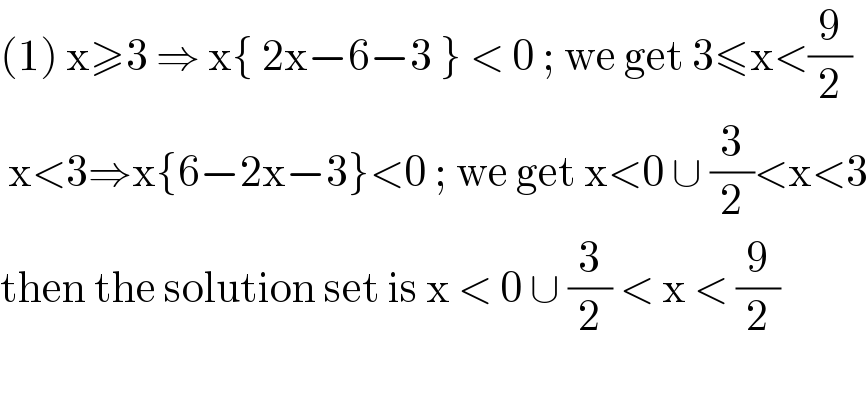
$$\left(\mathrm{1}\right)\:\mathrm{x}\geqslant\mathrm{3}\:\Rightarrow\:\mathrm{x}\left\{\:\mathrm{2x}−\mathrm{6}−\mathrm{3}\:\right\}\:<\:\mathrm{0}\:;\:\mathrm{we}\:\mathrm{get}\:\mathrm{3}\leqslant\mathrm{x}<\frac{\mathrm{9}}{\mathrm{2}} \\ $$$$\:\mathrm{x}<\mathrm{3}\Rightarrow\mathrm{x}\left\{\mathrm{6}−\mathrm{2x}−\mathrm{3}\right\}<\mathrm{0}\:;\:\mathrm{we}\:\mathrm{get}\:\mathrm{x}<\mathrm{0}\:\cup\:\frac{\mathrm{3}}{\mathrm{2}}<\mathrm{x}<\mathrm{3} \\ $$$$\mathrm{then}\:\mathrm{the}\:\mathrm{solution}\:\mathrm{set}\:\mathrm{is}\:\mathrm{x}\:<\:\mathrm{0}\:\cup\:\frac{\mathrm{3}}{\mathrm{2}}\:<\:\mathrm{x}\:<\:\frac{\mathrm{9}}{\mathrm{2}} \\ $$$$ \\ $$
