Question Number 115230 by bemath last updated on 24/Sep/20

$$\mathrm{2}\:{women}\:{and}\:\mathrm{4}\:{men}\:{will}\:{sit}\:{on}\:{the} \\ $$$$\mathrm{8}\:{available}\:{seats}\:{and}\:{surround}\: \\ $$$${the}\:{round}\:{table}\:.\:{The}\:{many}\:{possible} \\ $$$${arrangements}\:{of}\:{them}\:{sitting} \\ $$$${if}\:{they}\:{sat}\:{randomly} \\ $$
Commented by mr W last updated on 24/Sep/20

$${P}_{\mathrm{5}} ^{\mathrm{7}} =\mathrm{2520} \\ $$$${or}\:{C}_{\mathrm{5}} ^{\mathrm{7}} ×\mathrm{5}! \\ $$
Commented by bemath last updated on 24/Sep/20
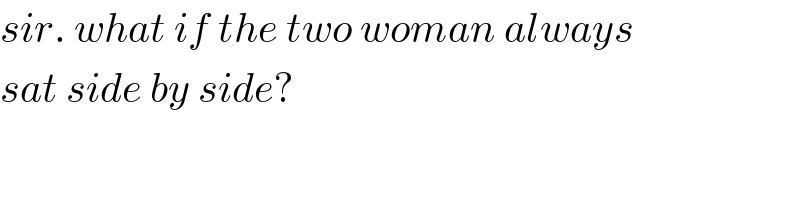
$${sir}.\:{what}\:{if}\:{the}\:{two}\:{woman}\:{always} \\ $$$${sat}\:{side}\:{by}\:{side}? \\ $$
Commented by bemath last updated on 24/Sep/20
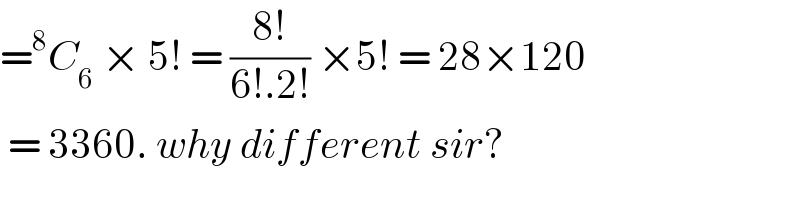
$$=^{\mathrm{8}} {C}_{\mathrm{6}} \:×\:\mathrm{5}!\:=\:\frac{\mathrm{8}!}{\mathrm{6}!.\mathrm{2}!}\:×\mathrm{5}!\:=\:\mathrm{28}×\mathrm{120} \\ $$$$\:=\:\mathrm{3360}.\:{why}\:{different}\:{sir}? \\ $$
Commented by mr W last updated on 24/Sep/20

$$\mathrm{2}×{P}_{\mathrm{4}} ^{\mathrm{6}} =\mathrm{720} \\ $$
Commented by mr W last updated on 24/Sep/20

$${to}\:{select}\:\mathrm{6}\:{seats}\:{from}\:\mathrm{8}\:{seats}\:{on}\:{a} \\ $$$${round}\:{table}\:{there}\:{are}\:{C}_{\mathrm{5}} ^{\mathrm{7}} \:{ways},\:{not} \\ $$$${C}_{\mathrm{6}} ^{\mathrm{8}} \:{ways}!\:{because}\:{the}\:“{absolute}''\: \\ $$$${positions}\:{of}\:{the}\:{seats}\:{are}\:{not}\:{important}, \\ $$$${but}\:{only}\:{the}\:“{relative}''\:{positions}\:{of} \\ $$$${them}.\:{that}\:{means}\:{you}\:{can}\:{fix}\:{one} \\ $$$${seat}\:{and}\:{select}\:\mathrm{5}\:{from}\:{the}\:{remaining} \\ $$$$\mathrm{7}\:{seats},\:{you}\:{have}\:{C}_{\mathrm{5}} ^{\mathrm{7}} \:{ways}\:{to}\:{do}\:{this}. \\ $$
Commented by bemath last updated on 25/Sep/20
$${thank}\:{you}\:{prof}\:{for}\:{explanation} \\ $$
