Question Number 148011 by puissant last updated on 25/Jul/21
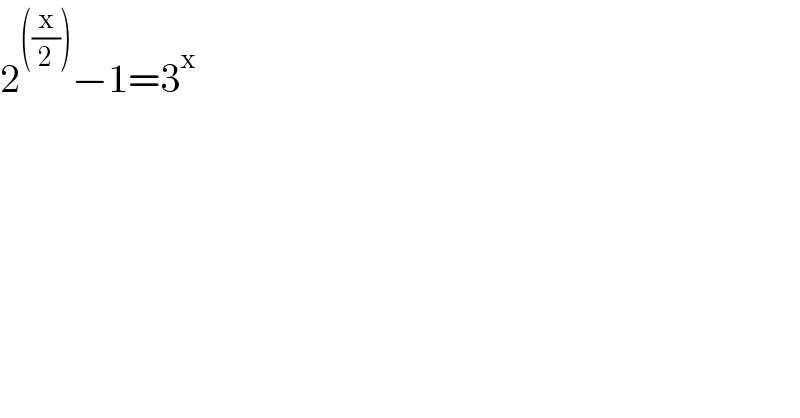
$$\mathrm{2}^{\left(\frac{\mathrm{x}}{\mathrm{2}}\right)} −\mathrm{1}=\mathrm{3}^{\mathrm{x}} \\ $$
Commented by mr W last updated on 25/Jul/21
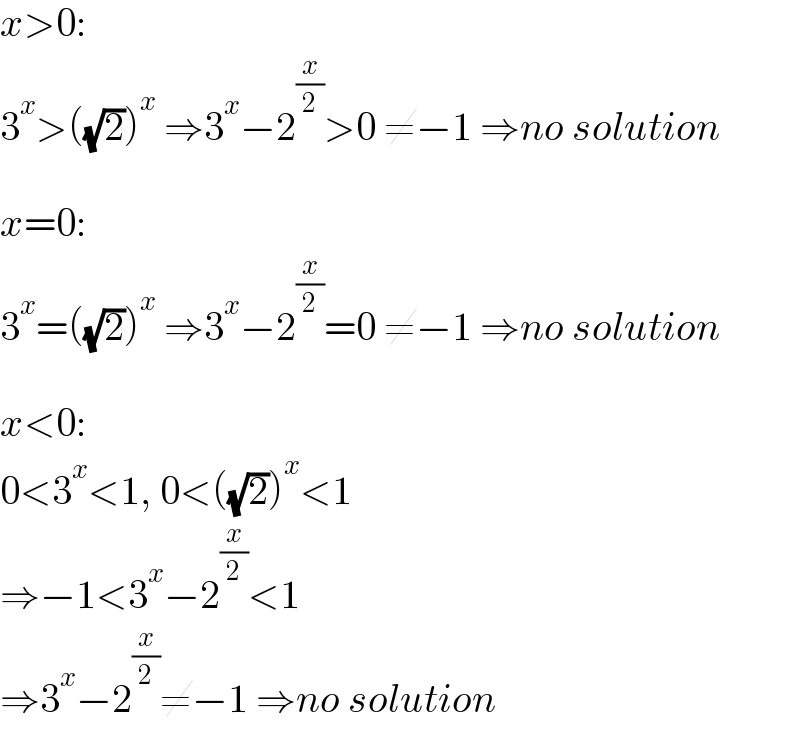
$${x}>\mathrm{0}:\: \\ $$$$\mathrm{3}^{{x}} >\left(\sqrt{\mathrm{2}}\right)^{{x}} \:\Rightarrow\mathrm{3}^{{x}} −\mathrm{2}^{\frac{{x}}{\mathrm{2}}} >\mathrm{0}\:\neq−\mathrm{1}\:\Rightarrow{no}\:{solution} \\ $$$$ \\ $$$${x}=\mathrm{0}: \\ $$$$\mathrm{3}^{{x}} =\left(\sqrt{\mathrm{2}}\right)^{{x}} \:\Rightarrow\mathrm{3}^{{x}} −\mathrm{2}^{\frac{{x}}{\mathrm{2}}} =\mathrm{0}\:\neq−\mathrm{1}\:\Rightarrow{no}\:{solution} \\ $$$$ \\ $$$${x}<\mathrm{0}: \\ $$$$\mathrm{0}<\mathrm{3}^{{x}} <\mathrm{1},\:\mathrm{0}<\left(\sqrt{\mathrm{2}}\right)^{{x}} <\mathrm{1} \\ $$$$\Rightarrow−\mathrm{1}<\mathrm{3}^{{x}} −\mathrm{2}^{\frac{{x}}{\mathrm{2}}} <\mathrm{1} \\ $$$$\Rightarrow\mathrm{3}^{{x}} −\mathrm{2}^{\frac{{x}}{\mathrm{2}}} \neq−\mathrm{1}\:\Rightarrow{no}\:{solution} \\ $$
