Menu Close

2-x-2-1-x-1-x-2-dx-

Tinku Tara 0 Comments
Pin




Question Number 91086 by jagoll last updated on 28/Apr/20
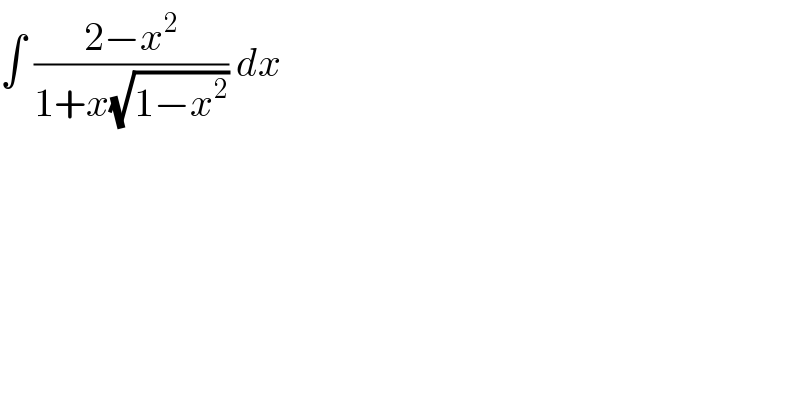
∫ ((2−x^2 )/(1+x(√(1−x^2 )))) dx
$$\int\:\frac{\mathrm{2}−{x}^{\mathrm{2}} }{\mathrm{1}+{x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:{dx}\: \\ $$
Answered by MJS last updated on 28/Apr/20
∫((2−x^2 )/(1+x(√(1−x^2 ))))dx= the two necessary steps in one: x=sin θ ∧ θ=2arctan t ⇒ x=((2t)/(t^2 +1)) t=((1+(√(1−x^2 )))/x) → dx=−((x^2 (√(1−x^2 )))/(1+(√(1−x^2 ))))dt=−((2(t^2 −1))/((t^2 +1)^2 ))dt =−4∫(((t^2 −1)(t^4 +1))/((t^2 +1)^2 (t^4 +2t^3 +2t^2 −2t+1)))dt= t^4 +2t^3 +2t^2 −2t+1=(t^2 +(1−(√3))t+2−(√3))(t^2 +(1+(√3))t+2+(√3)) =4∫(t/((t^2 +1)^2 ))dt−∫(((√3)t−1)/(t^2 +(1−(√3))t+2−(√3)))dt+∫(((√3)t+1)/(t^2 +(1+(√3))t+2+(√3)))dt= =−(2/(t^2 +1))+((√3)/2)ln ((t^2 +(1+(√3))t+2+(√3))/(t^2 +(1−(√3))t+2−(√3))) +arctan ((1−(√3))t−1) +arctan ((1+(√3))t+1) = =−(x^2 /(1+(√(1−x^2 ))))+((√3)/2)ln ((x^2 −2+(√(3(1−x^2 ))))/(x^2 −(√3)x+1)) +arctan (((1−(√3))(1+(√(1−x^2 )))−x)/x) +arctan (((1+(√3))(1+(√(1−x^2 )))−x)/x) +C I found no easier path I hope I made no typos...
$$\int\frac{\mathrm{2}−{x}^{\mathrm{2}} }{\mathrm{1}+{x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx}= \\ $$$$\:\:\:\:\:\mathrm{the}\:\mathrm{two}\:\mathrm{necessary}\:\mathrm{steps}\:\mathrm{in}\:\mathrm{one}: \\ $$$$\:\:\:\:\:{x}=\mathrm{sin}\:\theta\:\wedge\:\theta=\mathrm{2arctan}\:{t}\:\Rightarrow\:{x}=\frac{\mathrm{2}{t}}{{t}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\:\:\:\:\:{t}=\frac{\mathrm{1}+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{{x}}\:\rightarrow\:{dx}=−\frac{{x}^{\mathrm{2}} \sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{\mathrm{1}+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dt}=−\frac{\mathrm{2}\left({t}^{\mathrm{2}} −\mathrm{1}\right)}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dt} \\ $$$$=−\mathrm{4}\int\frac{\left({t}^{\mathrm{2}} −\mathrm{1}\right)\left({t}^{\mathrm{4}} +\mathrm{1}\right)}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} \left({t}^{\mathrm{4}} +\mathrm{2}{t}^{\mathrm{3}} +\mathrm{2}{t}^{\mathrm{2}} −\mathrm{2}{t}+\mathrm{1}\right)}{dt}= \\ $$$$\:\:\:\:\:{t}^{\mathrm{4}} +\mathrm{2}{t}^{\mathrm{3}} +\mathrm{2}{t}^{\mathrm{2}} −\mathrm{2}{t}+\mathrm{1}=\left({t}^{\mathrm{2}} +\left(\mathrm{1}−\sqrt{\mathrm{3}}\right){t}+\mathrm{2}−\sqrt{\mathrm{3}}\right)\left({t}^{\mathrm{2}} +\left(\mathrm{1}+\sqrt{\mathrm{3}}\right){t}+\mathrm{2}+\sqrt{\mathrm{3}}\right) \\ $$$$=\mathrm{4}\int\frac{{t}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dt}−\int\frac{\sqrt{\mathrm{3}}{t}−\mathrm{1}}{{t}^{\mathrm{2}} +\left(\mathrm{1}−\sqrt{\mathrm{3}}\right){t}+\mathrm{2}−\sqrt{\mathrm{3}}}{dt}+\int\frac{\sqrt{\mathrm{3}}{t}+\mathrm{1}}{{t}^{\mathrm{2}} +\left(\mathrm{1}+\sqrt{\mathrm{3}}\right){t}+\mathrm{2}+\sqrt{\mathrm{3}}}{dt}= \\ $$$$=−\frac{\mathrm{2}}{{t}^{\mathrm{2}} +\mathrm{1}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{ln}\:\frac{{t}^{\mathrm{2}} +\left(\mathrm{1}+\sqrt{\mathrm{3}}\right){t}+\mathrm{2}+\sqrt{\mathrm{3}}}{{t}^{\mathrm{2}} +\left(\mathrm{1}−\sqrt{\mathrm{3}}\right){t}+\mathrm{2}−\sqrt{\mathrm{3}}}\:+\mathrm{arctan}\:\left(\left(\mathrm{1}−\sqrt{\mathrm{3}}\right){t}−\mathrm{1}\right)\:+\mathrm{arctan}\:\left(\left(\mathrm{1}+\sqrt{\mathrm{3}}\right){t}+\mathrm{1}\right)\:= \\ $$$$=−\frac{{x}^{\mathrm{2}} }{\mathrm{1}+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{ln}\:\frac{{x}^{\mathrm{2}} −\mathrm{2}+\sqrt{\mathrm{3}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}}{{x}^{\mathrm{2}} −\sqrt{\mathrm{3}}{x}+\mathrm{1}}\:+\mathrm{arctan}\:\frac{\left(\mathrm{1}−\sqrt{\mathrm{3}}\right)\left(\mathrm{1}+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\right)−{x}}{{x}}\:+\mathrm{arctan}\:\frac{\left(\mathrm{1}+\sqrt{\mathrm{3}}\right)\left(\mathrm{1}+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\right)−{x}}{{x}}\:+{C} \\ $$$$\mathrm{I}\:\mathrm{found}\:\mathrm{no}\:\mathrm{easier}\:\mathrm{path} \\ $$$$\mathrm{I}\:\mathrm{hope}\:\mathrm{I}\:\mathrm{made}\:\mathrm{no}\:\mathrm{typos}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *