Question Number 53912 by Mikael_Marshall last updated on 27/Jan/19
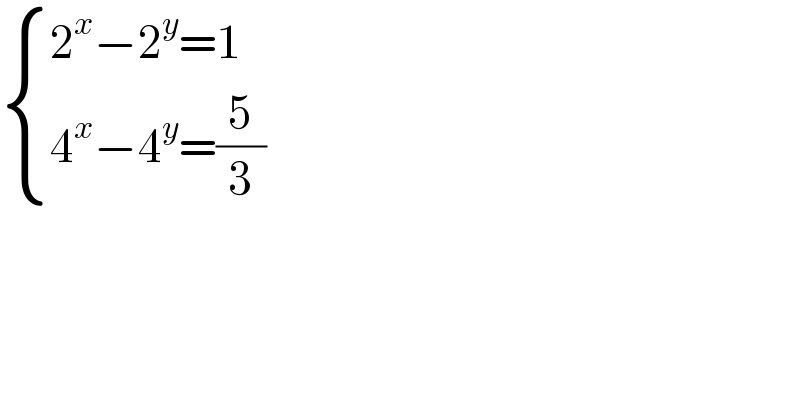
$$\begin{cases}{\mathrm{2}^{{x}} −\mathrm{2}^{{y}} =\mathrm{1}}\\{\mathrm{4}^{{x}} −\mathrm{4}^{{y}} =\frac{\mathrm{5}}{\mathrm{3}}}\end{cases} \\ $$
Answered by byaw last updated on 27/Jan/19
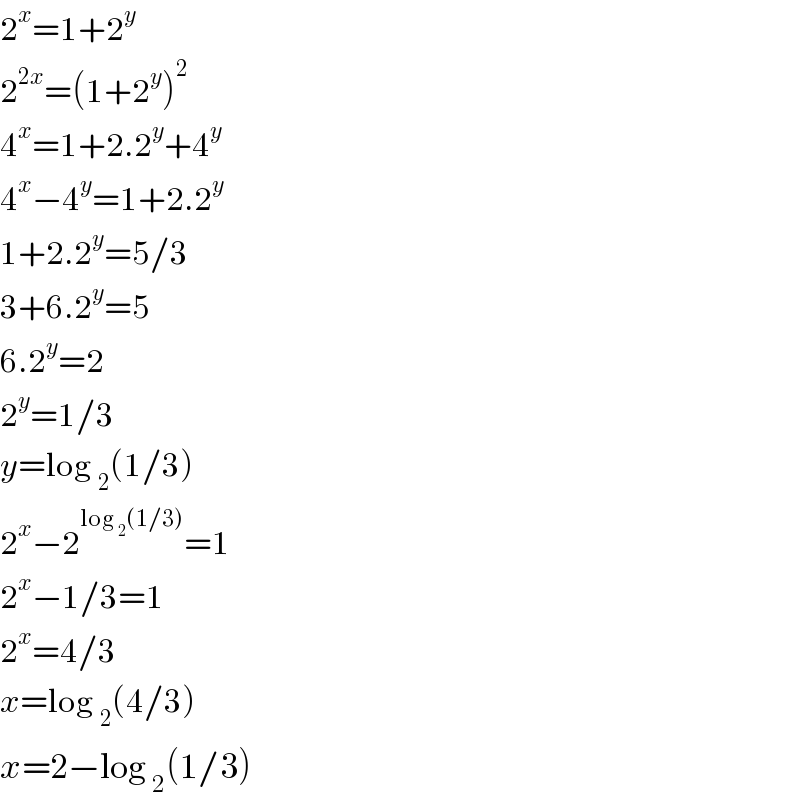
$$\mathrm{2}^{{x}} =\mathrm{1}+\mathrm{2}^{{y}} \\ $$$$\mathrm{2}^{\mathrm{2}{x}} =\left(\mathrm{1}+\mathrm{2}^{{y}} \right)^{\mathrm{2}} \\ $$$$\mathrm{4}^{{x}} =\mathrm{1}+\mathrm{2}.\mathrm{2}^{{y}} +\mathrm{4}^{{y}} \\ $$$$\mathrm{4}^{{x}} −\mathrm{4}^{{y}} =\mathrm{1}+\mathrm{2}.\mathrm{2}^{{y}} \\ $$$$\mathrm{1}+\mathrm{2}.\mathrm{2}^{{y}} =\mathrm{5}/\mathrm{3} \\ $$$$\mathrm{3}+\mathrm{6}.\mathrm{2}^{{y}} =\mathrm{5} \\ $$$$\mathrm{6}.\mathrm{2}^{{y}} =\mathrm{2} \\ $$$$\mathrm{2}^{{y}} =\mathrm{1}/\mathrm{3} \\ $$$${y}=\mathrm{log}\:_{\mathrm{2}} \left(\mathrm{1}/\mathrm{3}\right) \\ $$$$\mathrm{2}^{{x}} −\mathrm{2}^{\mathrm{log}\:_{\mathrm{2}} \left(\mathrm{1}/\mathrm{3}\right)} =\mathrm{1} \\ $$$$\mathrm{2}^{{x}} −\mathrm{1}/\mathrm{3}=\mathrm{1} \\ $$$$\mathrm{2}^{{x}} =\mathrm{4}/\mathrm{3} \\ $$$${x}=\mathrm{log}\:_{\mathrm{2}} \left(\mathrm{4}/\mathrm{3}\right) \\ $$$${x}=\mathrm{2}−\mathrm{log}\:_{\mathrm{2}} \left(\mathrm{1}/\mathrm{3}\right) \\ $$
Commented by Mikael_Marshall last updated on 27/Jan/19

$${thanks}\:{Sir}! \\ $$
Commented by JDamian last updated on 27/Jan/19

$$ \\ $$$$\mathrm{Hi},\:\boldsymbol{\mathrm{byaw}}.\:\mathrm{Your}\:\mathrm{last}\:\mathrm{line}\:\mathrm{is}\:\mathrm{wrong}.\:\mathrm{It}\:\mathrm{should}\:\mathrm{be} \\ $$$$\:\:\:{x}=\mathrm{2}−\mathrm{log}_{\mathrm{2}} \mathrm{3} \\ $$
Commented by byaw last updated on 15/Feb/19

$${yes}\:{I}\:{ve}\:{realized} \\ $$
Answered by peter frank last updated on 27/Jan/19
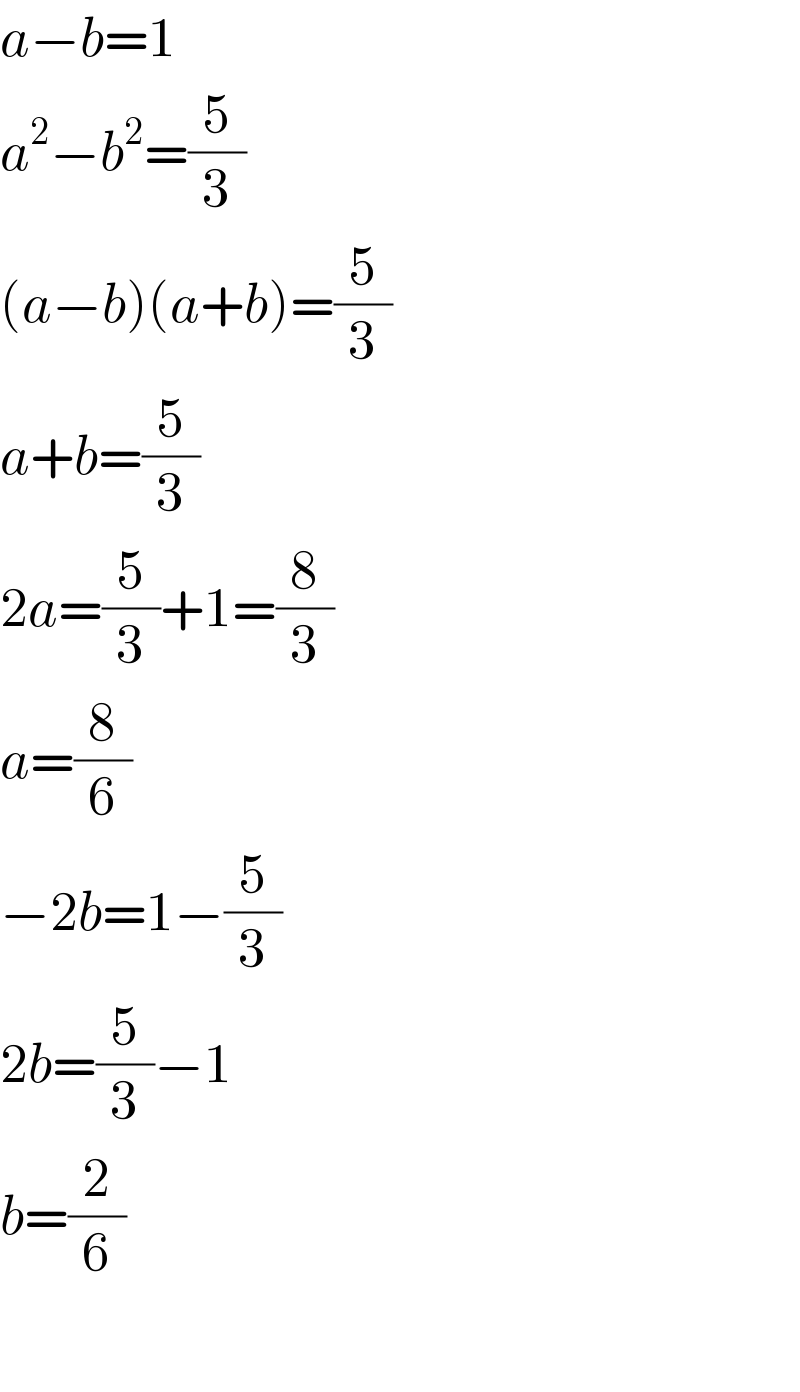
$${a}−{b}=\mathrm{1} \\ $$$${a}^{\mathrm{2}} −{b}^{\mathrm{2}} =\frac{\mathrm{5}}{\mathrm{3}} \\ $$$$\left({a}−{b}\right)\left({a}+{b}\right)=\frac{\mathrm{5}}{\mathrm{3}} \\ $$$${a}+{b}=\frac{\mathrm{5}}{\mathrm{3}} \\ $$$$\mathrm{2}{a}=\frac{\mathrm{5}}{\mathrm{3}}+\mathrm{1}=\frac{\mathrm{8}}{\mathrm{3}} \\ $$$${a}=\frac{\mathrm{8}}{\mathrm{6}} \\ $$$$−\mathrm{2}{b}=\mathrm{1}−\frac{\mathrm{5}}{\mathrm{3}} \\ $$$$\mathrm{2}{b}=\frac{\mathrm{5}}{\mathrm{3}}−\mathrm{1} \\ $$$${b}=\frac{\mathrm{2}}{\mathrm{6}} \\ $$$$ \\ $$
Commented by Mikael_Marshall last updated on 27/Jan/19

$${thanks}\:{Sir} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 27/Jan/19
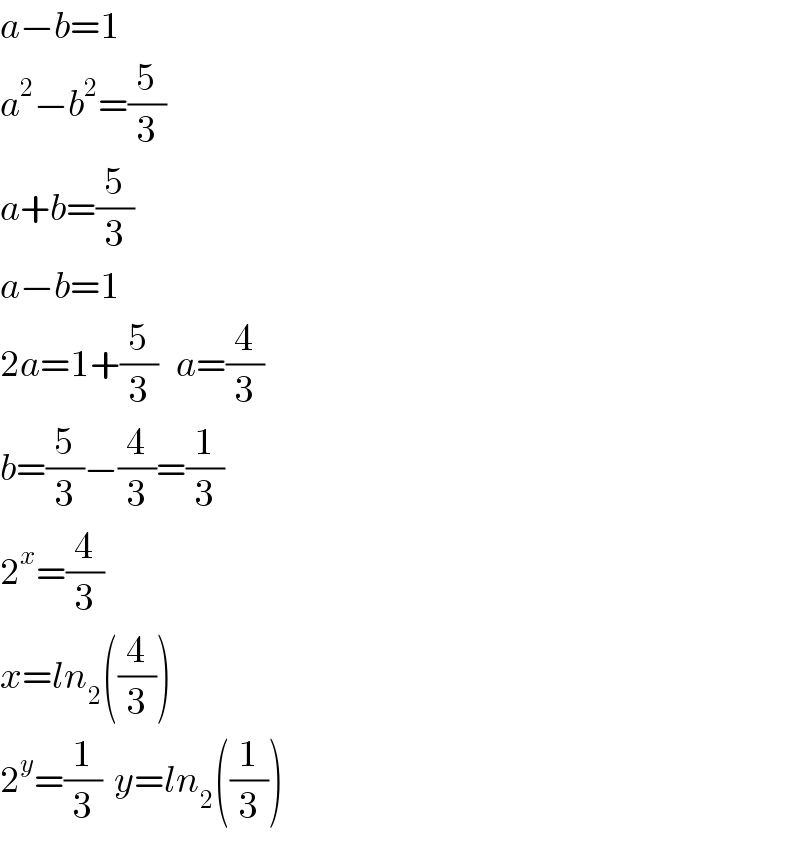
$${a}−{b}=\mathrm{1} \\ $$$${a}^{\mathrm{2}} −{b}^{\mathrm{2}} =\frac{\mathrm{5}}{\mathrm{3}} \\ $$$${a}+{b}=\frac{\mathrm{5}}{\mathrm{3}} \\ $$$${a}−{b}=\mathrm{1} \\ $$$$\mathrm{2}{a}=\mathrm{1}+\frac{\mathrm{5}}{\mathrm{3}}\:\:\:{a}=\frac{\mathrm{4}}{\mathrm{3}} \\ $$$${b}=\frac{\mathrm{5}}{\mathrm{3}}−\frac{\mathrm{4}}{\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\mathrm{2}^{{x}} =\frac{\mathrm{4}}{\mathrm{3}} \\ $$$${x}={ln}_{\mathrm{2}} \left(\frac{\mathrm{4}}{\mathrm{3}}\right) \\ $$$$\mathrm{2}^{{y}} =\frac{\mathrm{1}}{\mathrm{3}}\:\:{y}={ln}_{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$
