Question Number 82577 by M±th+et£s last updated on 22/Feb/20
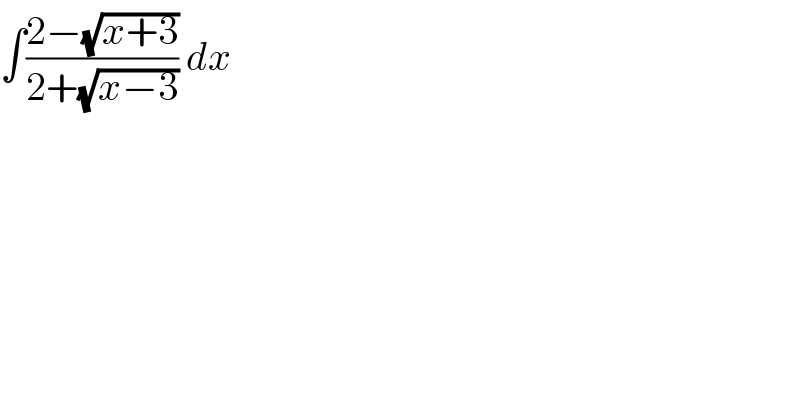
$$\int\frac{\mathrm{2}−\sqrt{{x}+\mathrm{3}}}{\mathrm{2}+\sqrt{{x}−\mathrm{3}}}\:{dx} \\ $$
Commented by mathmax by abdo last updated on 22/Feb/20
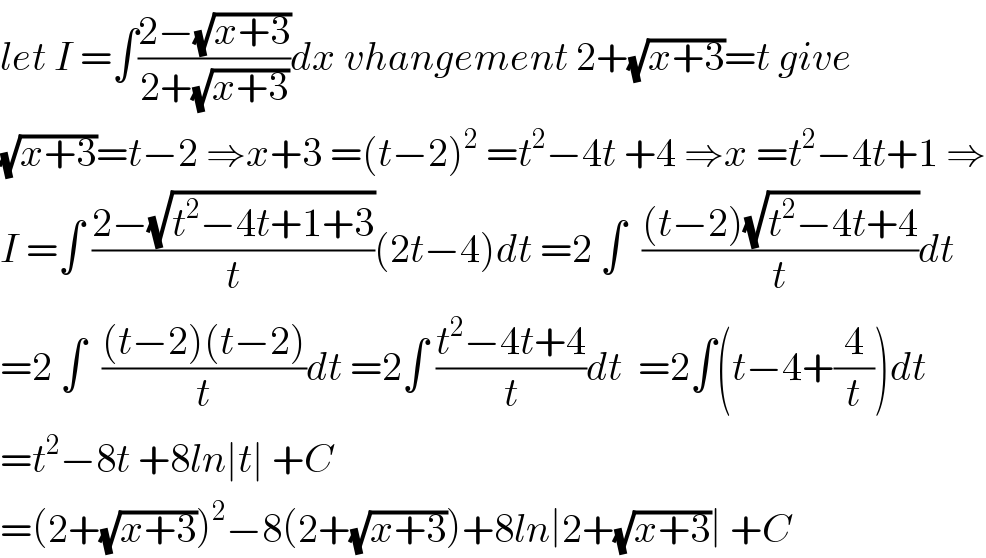
$${let}\:{I}\:=\int\frac{\mathrm{2}−\sqrt{{x}+\mathrm{3}}}{\mathrm{2}+\sqrt{{x}+\mathrm{3}}}{dx}\:{vhangement}\:\mathrm{2}+\sqrt{{x}+\mathrm{3}}={t}\:{give} \\ $$$$\sqrt{{x}+\mathrm{3}}={t}−\mathrm{2}\:\Rightarrow{x}+\mathrm{3}\:=\left({t}−\mathrm{2}\right)^{\mathrm{2}} \:={t}^{\mathrm{2}} −\mathrm{4}{t}\:+\mathrm{4}\:\Rightarrow{x}\:={t}^{\mathrm{2}} −\mathrm{4}{t}+\mathrm{1}\:\Rightarrow \\ $$$${I}\:=\int\:\frac{\mathrm{2}−\sqrt{{t}^{\mathrm{2}} −\mathrm{4}{t}+\mathrm{1}+\mathrm{3}}}{{t}}\left(\mathrm{2}{t}−\mathrm{4}\right){dt}\:=\mathrm{2}\:\int\:\:\frac{\left({t}−\mathrm{2}\right)\sqrt{{t}^{\mathrm{2}} −\mathrm{4}{t}+\mathrm{4}}}{{t}}{dt} \\ $$$$=\mathrm{2}\:\int\:\:\frac{\left({t}−\mathrm{2}\right)\left({t}−\mathrm{2}\right)}{{t}}{dt}\:=\mathrm{2}\int\:\frac{{t}^{\mathrm{2}} −\mathrm{4}{t}+\mathrm{4}}{{t}}{dt}\:\:=\mathrm{2}\int\left({t}−\mathrm{4}+\frac{\mathrm{4}}{{t}}\right){dt} \\ $$$$={t}^{\mathrm{2}} −\mathrm{8}{t}\:+\mathrm{8}{ln}\mid{t}\mid\:+{C} \\ $$$$=\left(\mathrm{2}+\sqrt{{x}+\mathrm{3}}\right)^{\mathrm{2}} −\mathrm{8}\left(\mathrm{2}+\sqrt{{x}+\mathrm{3}}\right)+\mathrm{8}{ln}\mid\mathrm{2}+\sqrt{{x}+\mathrm{3}}\mid\:+{C} \\ $$
Commented by M±th+et£s last updated on 22/Feb/20

$${god}\:{bless}\:{you}\:{sir} \\ $$
Commented by msup trace by abdo last updated on 22/Feb/20

$${thank}\:{you}\:{sir}. \\ $$
