Question Number 39477 by malwaan last updated on 06/Jul/18
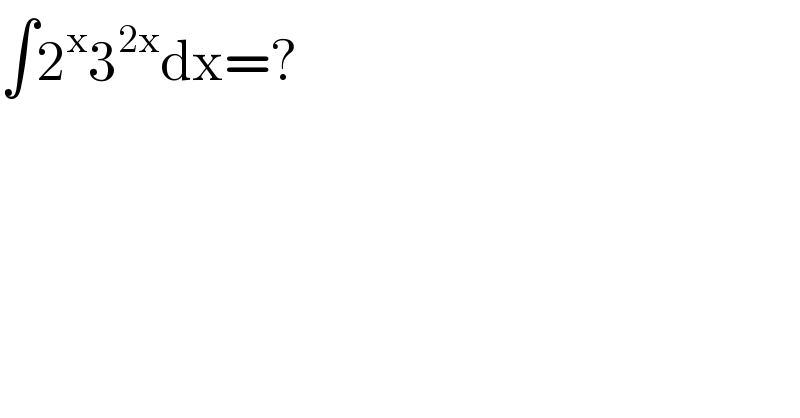
$$\int\mathrm{2}^{\mathrm{x}} \mathrm{3}^{\mathrm{2x}} \mathrm{dx}=? \\ $$
Commented by abdo mathsup 649 cc last updated on 07/Jul/18
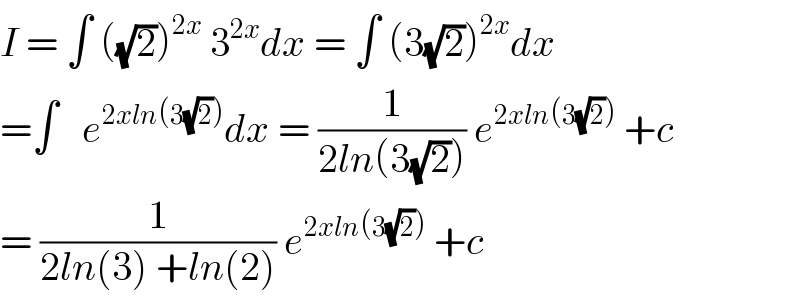
$${I}\:=\:\int\:\left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}{x}} \:\mathrm{3}^{\mathrm{2}{x}} {dx}\:=\:\int\:\left(\mathrm{3}\sqrt{\mathrm{2}}\right)^{\mathrm{2}{x}} {dx} \\ $$$$=\int\:\:\:{e}^{\mathrm{2}{xln}\left(\mathrm{3}\sqrt{\mathrm{2}}\right)} {dx}\:=\:\frac{\mathrm{1}}{\mathrm{2}{ln}\left(\mathrm{3}\sqrt{\mathrm{2}}\right)}\:{e}^{\mathrm{2}{xln}\left(\mathrm{3}\sqrt{\mathrm{2}}\right)} \:+{c} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}{ln}\left(\mathrm{3}\right)\:+{ln}\left(\mathrm{2}\right)}\:{e}^{\mathrm{2}{xln}\left(\mathrm{3}\sqrt{\mathrm{2}}\right)} \:+{c}\: \\ $$
Commented by math1967 last updated on 08/Jul/18

$${Easy}\:{method}\:{sir} \\ $$
Commented by malwaan last updated on 13/Jul/18
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much} \\ $$
Answered by math1967 last updated on 06/Jul/18
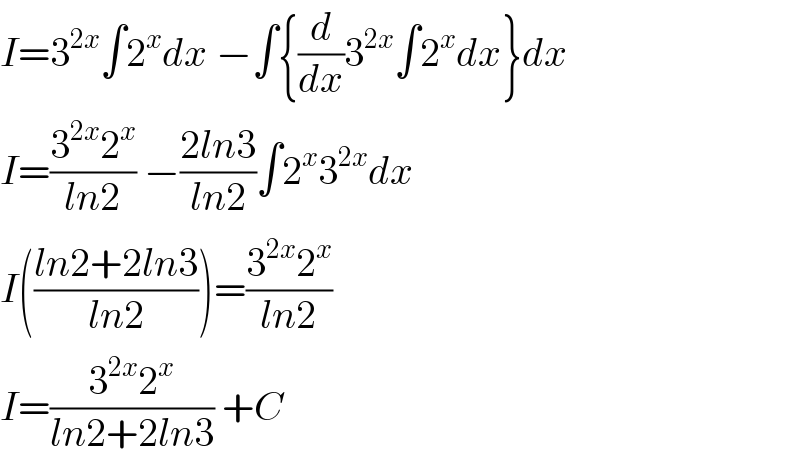
$${I}=\mathrm{3}^{\mathrm{2}{x}} \int\mathrm{2}^{{x}} {dx}\:−\int\left\{\frac{{d}}{{dx}}\mathrm{3}^{\mathrm{2}{x}} \int\mathrm{2}^{{x}} {dx}\right\}{dx} \\ $$$${I}=\frac{\mathrm{3}^{\mathrm{2}{x}} \mathrm{2}^{{x}} }{{ln}\mathrm{2}}\:−\frac{\mathrm{2}{ln}\mathrm{3}}{{ln}\mathrm{2}}\int\mathrm{2}^{{x}} \mathrm{3}^{\mathrm{2}{x}} {dx} \\ $$$${I}\left(\frac{{ln}\mathrm{2}+\mathrm{2}{ln}\mathrm{3}}{{ln}\mathrm{2}}\right)=\frac{\mathrm{3}^{\mathrm{2}{x}} \mathrm{2}^{{x}} }{{ln}\mathrm{2}} \\ $$$${I}=\frac{\mathrm{3}^{\mathrm{2}{x}} \mathrm{2}^{{x}} }{{ln}\mathrm{2}+\mathrm{2}{ln}\mathrm{3}}\:+{C} \\ $$
Commented by malwaan last updated on 13/Jul/18
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}\: \\ $$
