2-x-3-4-x-48-x-

Question Number 168434 by mathlove last updated on 10/Apr/22

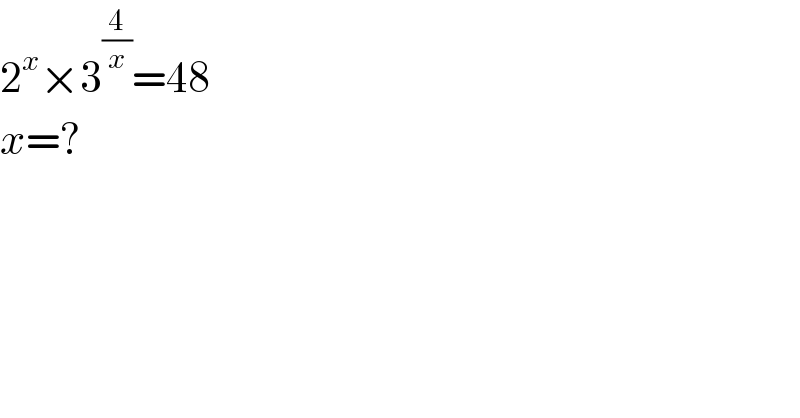
$$\mathrm{2}^{{x}} ×\mathrm{3}^{\frac{\mathrm{4}}{{x}}} =\mathrm{48} \\ $$$${x}=? \\ $$

Answered by nurtani last updated on 10/Apr/22

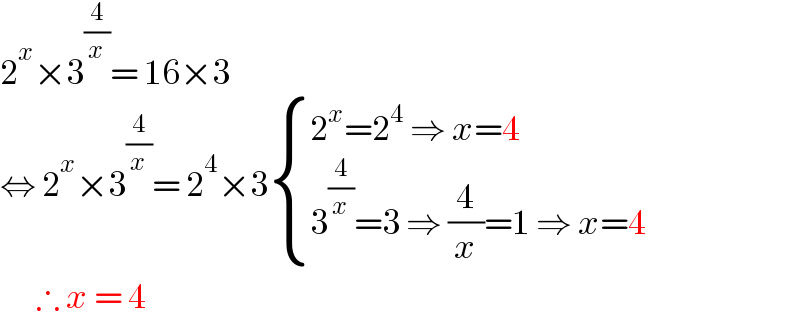
2^x ×3^(4/x) = 16×3 ⇔ 2^x ×3^(4/x) = 2^4 ×3 { ((2^x =2^4 ⇒ x=4)),((3^(4/x) =3 ⇒ (4/x)=1 ⇒ x=4)) :} ∴ x = 4

$$\mathrm{2}^{{x}} ×\mathrm{3}^{\frac{\mathrm{4}}{{x}}} =\:\mathrm{16}×\mathrm{3} \\ $$$$\Leftrightarrow\:\mathrm{2}^{{x}} ×\mathrm{3}^{\frac{\mathrm{4}}{{x}}} =\:\mathrm{2}^{\mathrm{4}} ×\mathrm{3\begin{cases}{\mathrm{2}^{{x}} =\mathrm{2}^{\mathrm{4}} \:\Rightarrow\:{x}=\mathrm{4}}\\{\mathrm{3}^{\frac{\mathrm{4}}{{x}}} =\mathrm{3}\:\Rightarrow\:\frac{\mathrm{4}}{{x}}=\mathrm{1}\:\Rightarrow\:{x}=\mathrm{4}}\end{cases}} \\ $$$$\:\:\:\:\:\:\therefore\:{x}\:=\:\mathrm{4} \\ $$

Answered by mr W last updated on 10/Apr/22

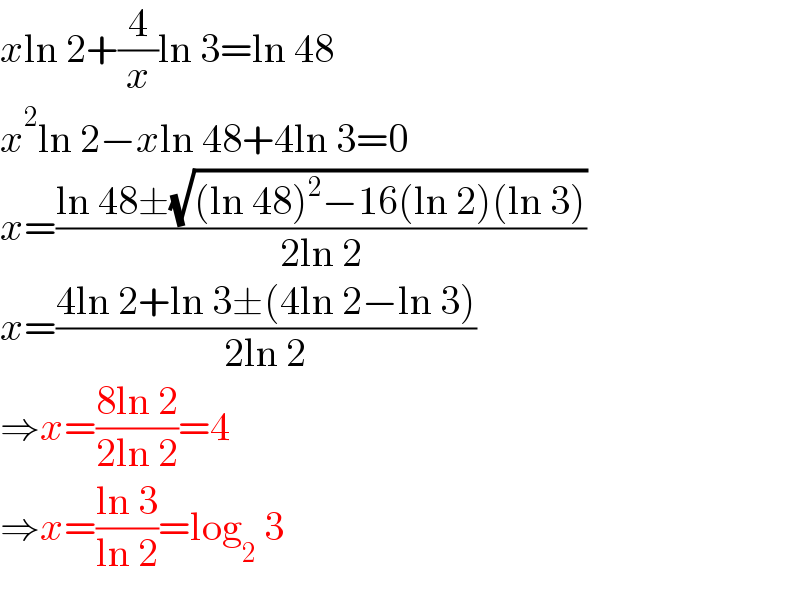
xln 2+(4/x)ln 3=ln 48 x^2 ln 2−xln 48+4ln 3=0 x=((ln 48±(√((ln 48)^2 −16(ln 2)(ln 3))))/(2ln 2)) x=((4ln 2+ln 3±(4ln 2−ln 3))/(2ln 2)) ⇒x=((8ln 2)/(2ln 2))=4 ⇒x=((ln 3)/(ln 2))=log_2 3

$${x}\mathrm{ln}\:\mathrm{2}+\frac{\mathrm{4}}{{x}}\mathrm{ln}\:\mathrm{3}=\mathrm{ln}\:\mathrm{48} \\ $$$${x}^{\mathrm{2}} \mathrm{ln}\:\mathrm{2}−{x}\mathrm{ln}\:\mathrm{48}+\mathrm{4ln}\:\mathrm{3}=\mathrm{0} \\ $$$${x}=\frac{\mathrm{ln}\:\mathrm{48}\pm\sqrt{\left(\mathrm{ln}\:\mathrm{48}\right)^{\mathrm{2}} −\mathrm{16}\left(\mathrm{ln}\:\mathrm{2}\right)\left(\mathrm{ln}\:\mathrm{3}\right)}}{\mathrm{2ln}\:\mathrm{2}} \\ $$$${x}=\frac{\mathrm{4ln}\:\mathrm{2}+\mathrm{ln}\:\mathrm{3}\pm\left(\mathrm{4ln}\:\mathrm{2}−\mathrm{ln}\:\mathrm{3}\right)}{\mathrm{2ln}\:\mathrm{2}} \\ $$$$\Rightarrow{x}=\frac{\mathrm{8ln}\:\mathrm{2}}{\mathrm{2ln}\:\mathrm{2}}=\mathrm{4} \\ $$$$\Rightarrow{x}=\frac{\mathrm{ln}\:\mathrm{3}}{\mathrm{ln}\:\mathrm{2}}=\mathrm{log}_{\mathrm{2}} \:\mathrm{3} \\ $$

Answered by cortano1 last updated on 11/Apr/22

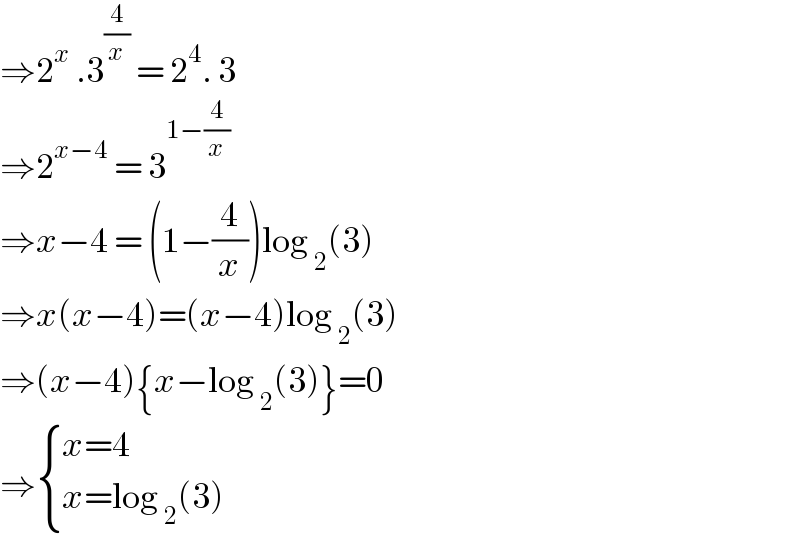
⇒2^x .3^(4/x) = 2^4 . 3 ⇒2^(x−4) = 3^(1−(4/x)) ⇒x−4 = (1−(4/x))log _2 (3) ⇒x(x−4)=(x−4)log _2 (3) ⇒(x−4){x−log _2 (3)}=0 ⇒ { ((x=4)),((x=log _2 (3))) :}

$$\Rightarrow\mathrm{2}^{{x}} \:.\mathrm{3}^{\frac{\mathrm{4}}{{x}}} \:=\:\mathrm{2}^{\mathrm{4}} .\:\mathrm{3} \\ $$$$\Rightarrow\mathrm{2}^{{x}−\mathrm{4}} \:=\:\mathrm{3}^{\mathrm{1}−\frac{\mathrm{4}}{{x}}} \\ $$$$\Rightarrow{x}−\mathrm{4}\:=\:\left(\mathrm{1}−\frac{\mathrm{4}}{{x}}\right)\mathrm{log}\:_{\mathrm{2}} \left(\mathrm{3}\right) \\ $$$$\Rightarrow{x}\left({x}−\mathrm{4}\right)=\left({x}−\mathrm{4}\right)\mathrm{log}\:_{\mathrm{2}} \left(\mathrm{3}\right) \\ $$$$\Rightarrow\left({x}−\mathrm{4}\right)\left\{{x}−\mathrm{log}\:_{\mathrm{2}} \left(\mathrm{3}\right)\right\}=\mathrm{0} \\ $$$$\Rightarrow\begin{cases}{{x}=\mathrm{4}}\\{{x}=\mathrm{log}\:_{\mathrm{2}} \left(\mathrm{3}\right)}\end{cases} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply