Menu Close

2-x-3-x-1-4-x-2-5-x-3-6-x-4-5-

Tinku Tara 0 Comments
Pin




Question Number 156063 by cortano last updated on 07/Oct/21
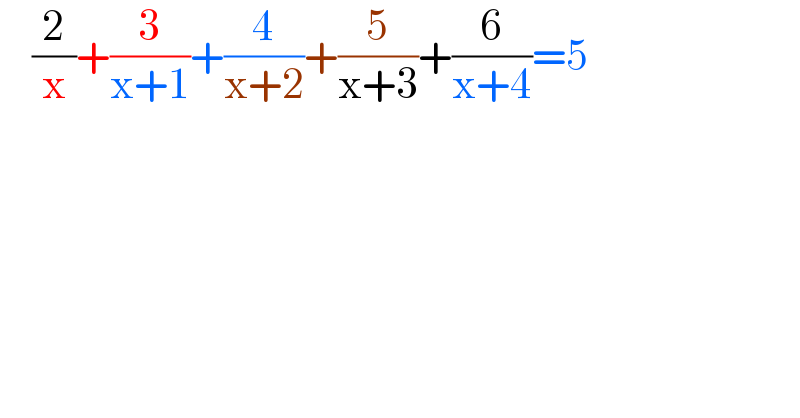
(2/x)+(3/(x+1))+(4/(x+2))+(5/(x+3))+(6/(x+4))=5
$$\:\:\:\:\frac{\mathrm{2}}{\mathrm{x}}+\frac{\mathrm{3}}{\mathrm{x}+\mathrm{1}}+\frac{\mathrm{4}}{\mathrm{x}+\mathrm{2}}+\frac{\mathrm{5}}{\mathrm{x}+\mathrm{3}}+\frac{\mathrm{6}}{\mathrm{x}+\mathrm{4}}=\mathrm{5} \\ $$
Commented by john_santu last updated on 07/Oct/21
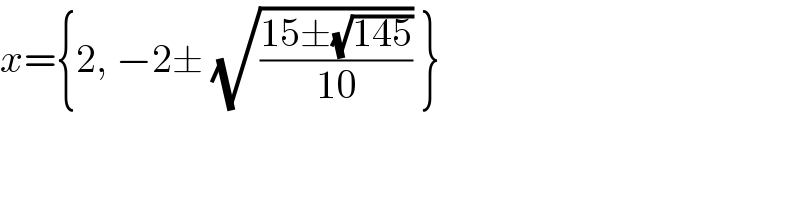
x={2, −2± (√((15±(√(145)))/(10))) }
$${x}=\left\{\mathrm{2},\:−\mathrm{2}\pm\:\sqrt{\frac{\mathrm{15}\pm\sqrt{\mathrm{145}}}{\mathrm{10}}}\:\right\} \\ $$
Commented by Tawa11 last updated on 07/Oct/21
nice
$$\mathrm{nice} \\ $$
Answered by ajfour last updated on 07/Oct/21
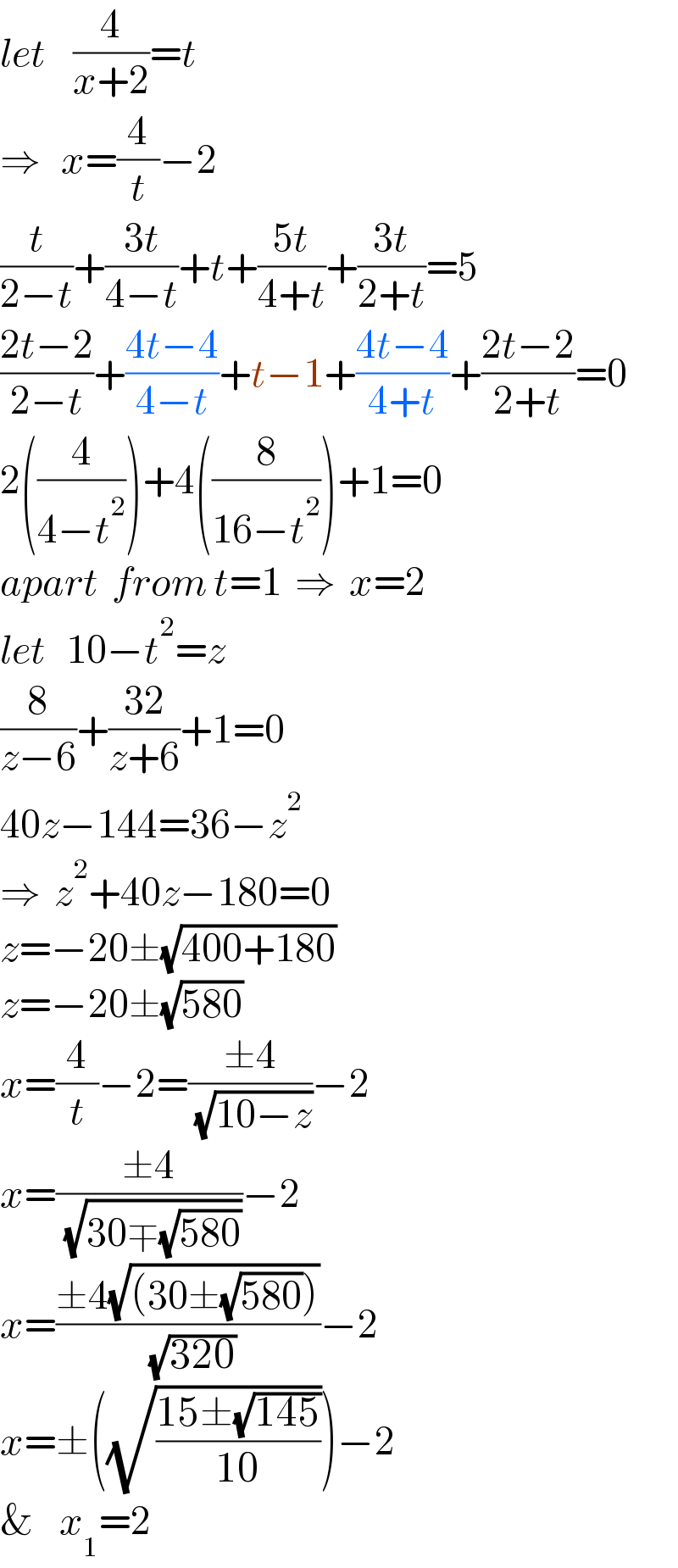
let (4/(x+2))=t ⇒ x=(4/t)−2 (t/(2−t))+((3t)/(4−t))+t+((5t)/(4+t))+((3t)/(2+t))=5 ((2t−2)/(2−t))+((4t−4)/(4−t))+t−1+((4t−4)/(4+t))+((2t−2)/(2+t))=0 2((4/(4−t^2 )))+4((8/(16−t^2 )))+1=0 apart from t=1 ⇒ x=2 let 10−t^2 =z (8/(z−6))+((32)/(z+6))+1=0 40z−144=36−z^2 ⇒ z^2 +40z−180=0 z=−20±(√(400+180)) z=−20±(√(580)) x=(4/t)−2=((±4)/( (√(10−z))))−2 x=((±4)/( (√(30∓(√(580))))))−2 x=((±4(√((30±(√(580))))))/( (√(320))))−2 x=±((√((15±(√(145)))/(10))))−2 & x_1 =2
$${let}\:\:\:\:\frac{\mathrm{4}}{{x}+\mathrm{2}}={t} \\ $$$$\Rightarrow\:\:\:{x}=\frac{\mathrm{4}}{{t}}−\mathrm{2} \\ $$$$\frac{{t}}{\mathrm{2}−{t}}+\frac{\mathrm{3}{t}}{\mathrm{4}−{t}}+{t}+\frac{\mathrm{5}{t}}{\mathrm{4}+{t}}+\frac{\mathrm{3}{t}}{\mathrm{2}+{t}}=\mathrm{5} \\ $$$$\frac{\mathrm{2}{t}−\mathrm{2}}{\mathrm{2}−{t}}+\frac{\mathrm{4}{t}−\mathrm{4}}{\mathrm{4}−{t}}+{t}−\mathrm{1}+\frac{\mathrm{4}{t}−\mathrm{4}}{\mathrm{4}+{t}}+\frac{\mathrm{2}{t}−\mathrm{2}}{\mathrm{2}+{t}}=\mathrm{0} \\ $$$$\mathrm{2}\left(\frac{\mathrm{4}}{\mathrm{4}−{t}^{\mathrm{2}} }\right)+\mathrm{4}\left(\frac{\mathrm{8}}{\mathrm{16}−{t}^{\mathrm{2}} }\right)+\mathrm{1}=\mathrm{0} \\ $$$${apart}\:\:{from}\:{t}=\mathrm{1}\:\:\Rightarrow\:\:{x}=\mathrm{2} \\ $$$${let}\:\:\:\mathrm{10}−{t}^{\mathrm{2}} ={z} \\ $$$$\frac{\mathrm{8}}{{z}−\mathrm{6}}+\frac{\mathrm{32}}{{z}+\mathrm{6}}+\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{40}{z}−\mathrm{144}=\mathrm{36}−{z}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:{z}^{\mathrm{2}} +\mathrm{40}{z}−\mathrm{180}=\mathrm{0} \\ $$$${z}=−\mathrm{20}\pm\sqrt{\mathrm{400}+\mathrm{180}} \\ $$$${z}=−\mathrm{20}\pm\sqrt{\mathrm{580}} \\ $$$${x}=\frac{\mathrm{4}}{{t}}−\mathrm{2}=\frac{\pm\mathrm{4}}{\:\sqrt{\mathrm{10}−{z}}}−\mathrm{2} \\ $$$${x}=\frac{\pm\mathrm{4}}{\:\sqrt{\mathrm{30}\mp\sqrt{\mathrm{580}}}}−\mathrm{2} \\ $$$${x}=\frac{\pm\mathrm{4}\sqrt{\left(\mathrm{30}\pm\sqrt{\mathrm{580}}\right)}}{\:\sqrt{\mathrm{320}}}−\mathrm{2} \\ $$$${x}=\pm\left(\sqrt{\frac{\mathrm{15}\pm\sqrt{\mathrm{145}}}{\mathrm{10}}}\right)−\mathrm{2} \\ $$$$\&\:\:\:{x}_{\mathrm{1}} =\mathrm{2} \\ $$
Commented by Tawa11 last updated on 08/Oct/21
Great sir
$$\mathrm{Great}\:\mathrm{sir} \\ $$
Answered by Rasheed.Sindhi last updated on 08/Oct/21
(2/x)+(3/(x+1))+(4/(x+2))+(5/(x+3))+(6/(x+4))=5 (2/x)−1+(3/(x+1))−1+(4/(x+2))−1+(5/(x+3))−1+(6/(x+4))−1=0 ((2−x)/x)+((3−x−1)/(x+1))+((4−x−2)/(x+2))+((5−x−3)/(x+3))+((6−x−4)/(x+4))=0 ((2−x)/x)+((2−x)/(x+1))+((2−x)/(x+2))+((2−x)/(x+3))+((2−x)/(x+4))=0 (2−x) ( (1/x)+(1/(x+1))+(1/(x+2))+(1/(x+3))+(1/(x+4)))=0 x=2 ∣ (1/x)+(1/(x+1))+(1/(x+2))+(1/(x+3))+(1/(x+4))=0 ((1/x)+(1/(x+4)))+((1/(x+1))+(1/(x+3)))+(1/(x+2)).((2(x+2))/(2(x+2)))=0 ((2x+4)/(x(x+4)))+((2x+4)/((x+1)(x+3)))+((2x+4)/(2(x+2)^2 ))=0 (1/(x(x+4)))+(1/((x+1)(x+3)))+(1/(2(x+2)^2 ))=0 [∵x≠−2] (1/(x^2 +4x))+(1/(x^2 +4x+3))+(1/(2(x^2 +4x+4)))=0 Let x^2 +4x=y (1/y)+(1/(y+3))+(1/(2(y+4)))=0 2(y+3)(y+4)+2y(y+4)+y(y+3)=0 2y^2 +14y+24+2y^2 +8y+y^2 +3y=0 5y^2 +25y+24=0 y=((−25±(√(625−480)))/(10)) x^2 +4x =((−25±(√(145)))/(10)) 10x^2 +40x+25∓(√(145)) =0 x=((−40±(√(1600−1000±40(√(145)))))/(20)) x=((−40±2(√(150±10(√(145)))))/(20)) x=((−20±(√(150±10(√(145)))))/(10)) =−2±(√((15±(√(145)))/(10))) , 2
$$ \\ $$$$\:\:\:\:\frac{\mathrm{2}}{\mathrm{x}}+\frac{\mathrm{3}}{\mathrm{x}+\mathrm{1}}+\frac{\mathrm{4}}{\mathrm{x}+\mathrm{2}}+\frac{\mathrm{5}}{\mathrm{x}+\mathrm{3}}+\frac{\mathrm{6}}{\mathrm{x}+\mathrm{4}}=\mathrm{5} \\ $$$$\:\:\:\:\frac{\mathrm{2}}{\mathrm{x}}−\mathrm{1}+\frac{\mathrm{3}}{\mathrm{x}+\mathrm{1}}−\mathrm{1}+\frac{\mathrm{4}}{\mathrm{x}+\mathrm{2}}−\mathrm{1}+\frac{\mathrm{5}}{\mathrm{x}+\mathrm{3}}−\mathrm{1}+\frac{\mathrm{6}}{\mathrm{x}+\mathrm{4}}−\mathrm{1}=\mathrm{0} \\ $$$$\:\:\:\:\frac{\mathrm{2}−\mathrm{x}}{\mathrm{x}}+\frac{\mathrm{3}−\mathrm{x}−\mathrm{1}}{\mathrm{x}+\mathrm{1}}+\frac{\mathrm{4}−\mathrm{x}−\mathrm{2}}{\mathrm{x}+\mathrm{2}}+\frac{\mathrm{5}−\mathrm{x}−\mathrm{3}}{\mathrm{x}+\mathrm{3}}+\frac{\mathrm{6}−\mathrm{x}−\mathrm{4}}{\mathrm{x}+\mathrm{4}}=\mathrm{0} \\ $$$$\:\:\:\:\frac{\mathrm{2}−\mathrm{x}}{\mathrm{x}}+\frac{\mathrm{2}−\mathrm{x}}{\mathrm{x}+\mathrm{1}}+\frac{\mathrm{2}−\mathrm{x}}{\mathrm{x}+\mathrm{2}}+\frac{\mathrm{2}−\mathrm{x}}{\mathrm{x}+\mathrm{3}}+\frac{\mathrm{2}−\mathrm{x}}{\mathrm{x}+\mathrm{4}}=\mathrm{0} \\ $$$$\:\:\left(\mathrm{2}−\mathrm{x}\right)\:\left(\:\frac{\mathrm{1}}{\mathrm{x}}+\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{x}+\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{x}+\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{x}+\mathrm{4}}\right)=\mathrm{0} \\ $$$$\mathrm{x}=\mathrm{2}\:\mid\:\frac{\mathrm{1}}{\mathrm{x}}+\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{x}+\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{x}+\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{x}+\mathrm{4}}=\mathrm{0} \\ $$$$\:\left(\frac{\mathrm{1}}{\mathrm{x}}+\frac{\mathrm{1}}{\mathrm{x}+\mathrm{4}}\right)+\left(\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{x}+\mathrm{3}}\right)+\frac{\mathrm{1}}{\mathrm{x}+\mathrm{2}}.\frac{\mathrm{2}\left(\mathrm{x}+\mathrm{2}\right)}{\mathrm{2}\left(\mathrm{x}+\mathrm{2}\right)}=\mathrm{0} \\ $$$$\frac{\mathrm{2x}+\mathrm{4}}{\mathrm{x}\left(\mathrm{x}+\mathrm{4}\right)}+\frac{\mathrm{2x}+\mathrm{4}}{\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}+\mathrm{3}\right)}+\frac{\mathrm{2x}+\mathrm{4}}{\mathrm{2}\left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{2}} }=\mathrm{0}\: \\ $$$$\:\:\:\:\frac{\mathrm{1}}{\mathrm{x}\left(\mathrm{x}+\mathrm{4}\right)}+\frac{\mathrm{1}}{\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}+\mathrm{3}\right)}+\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{2}} }=\mathrm{0}\:\left[\because\mathrm{x}\neq−\mathrm{2}\right] \\ $$$$\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{4x}}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{4x}+\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{4x}+\mathrm{4}\right)}=\mathrm{0} \\ $$$${Let}\:\mathrm{x}^{\mathrm{2}} +\mathrm{4x}=\mathrm{y} \\ $$$$\frac{\mathrm{1}}{\mathrm{y}}+\frac{\mathrm{1}}{\mathrm{y}+\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{y}+\mathrm{4}\right)}=\mathrm{0} \\ $$$$\mathrm{2}\left(\mathrm{y}+\mathrm{3}\right)\left(\mathrm{y}+\mathrm{4}\right)+\mathrm{2y}\left(\mathrm{y}+\mathrm{4}\right)+\mathrm{y}\left(\mathrm{y}+\mathrm{3}\right)=\mathrm{0} \\ $$$$\mathrm{2y}^{\mathrm{2}} +\mathrm{14y}+\mathrm{24}+\mathrm{2y}^{\mathrm{2}} +\mathrm{8y}+\mathrm{y}^{\mathrm{2}} +\mathrm{3y}=\mathrm{0} \\ $$$$\mathrm{5y}^{\mathrm{2}} +\mathrm{25y}+\mathrm{24}=\mathrm{0} \\ $$$$\mathrm{y}=\frac{−\mathrm{25}\pm\sqrt{\mathrm{625}−\mathrm{480}}}{\mathrm{10}} \\ $$$$\:\:\:\mathrm{x}^{\mathrm{2}} +\mathrm{4x}\:=\frac{−\mathrm{25}\pm\sqrt{\mathrm{145}}}{\mathrm{10}} \\ $$$$\:\:\mathrm{10x}^{\mathrm{2}} +\mathrm{40x}+\mathrm{25}\mp\sqrt{\mathrm{145}}\:=\mathrm{0} \\ $$$$\mathrm{x}=\frac{−\mathrm{40}\pm\sqrt{\mathrm{1600}−\mathrm{1000}\pm\mathrm{40}\sqrt{\mathrm{145}}}}{\mathrm{20}} \\ $$$$\mathrm{x}=\frac{−\mathrm{40}\pm\mathrm{2}\sqrt{\mathrm{150}\pm\mathrm{10}\sqrt{\mathrm{145}}}}{\mathrm{20}} \\ $$$$\mathrm{x}=\frac{−\mathrm{20}\pm\sqrt{\mathrm{150}\pm\mathrm{10}\sqrt{\mathrm{145}}}}{\mathrm{10}} \\ $$$$\:\:\:=−\mathrm{2}\pm\sqrt{\frac{\mathrm{15}\pm\sqrt{\mathrm{145}}}{\mathrm{10}}}\:\:,\:\mathrm{2} \\ $$
Answered by Rasheed.Sindhi last updated on 08/Oct/21
N^(A) E^(A^(S I^(⋏^•^∣ ) ) E) R WAY (2/x)+(3/(x+1))+(4/(x+2))+(5/(x+3))+(6/(x+4))=5 x+2=y: (2/(y−2))+(3/(y−1))+(4/y)+(5/(y+1))+(6/(y+2))=5 (2/(y−2))−1+(3/(y−1))−1+(4/y)−1+(5/(y+1))−1+(6/(y+2))−1=0 ((2−y+2)/(y−2))+((3−y+1)/(y−1))+((4−y)/y)+((5−y−1)/(y+1))+((6−y−2)/(y+2))=0 ((4−y)/(y−2))+((4−y)/(y−1))+((4−y)/y)+((4−y)/(y+1))+((4−y)/(y+2))=0 (4−y)((1/(y−2))+(1/(y−1))+(1/y)+(1/(y+1))+(1/(y+2)))=0 { ((4−y=0⇒y=4⇒x+2=4⇒x=2)),(((1/(y−2))+(1/(y−1))+(1/y)+(1/(y+1))+(1/(y+2))=0)) :} ((1/(y−2))+(1/(y+2)))+((1/(y−1))+(1/(y+1)))+(1/y)=0 ((2y)/(y^2 −4))+((2y)/(y^2 −1))+(1/y).((2y)/(2y))=0 2y((1/(y^2 −4))+(1/(y^2 −1))+(1/(2y^2 )))=0 (1/(y^2 −4))+(1/(y^2 −1))+(1/(2y^2 ))=0 [∵y≠0] (1/(y^2 −4))+(1/(y^2 −1))=((−1)/(2y^2 )) ((y^2 −1+y^2 −4)/((y^2 −4)(y^2 −1)))=((−1)/(2y^2 )) 2y^2 (2y^2 −5)=−(y^2 −4)(y^2 −1) 4y^4 −10y^2 =−y^4 +5y^2 −4 5y^4 −15y^2 +4=0 y^2 =((15±(√(225−80)))/(10))=((15±(√(145)))/(10)) (x+2)^2 =((15±(√(145)))/(10)) x=−2±(√((15±(√(145)))/(10))) x=2 , −2±(√((15±(√(145)))/(10)))
$$\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\overset{\mathbb{A}} {\mathbb{N}}\:\mathcal{E}^{\mathcal{A}^{\overset{\overset{\overset{\shortmid} {\bullet}} {\curlywedge}} {\mathcal{S}\:\:\mathcal{I}}} \mathcal{E}} \mathcal{R}\:\:\mathcal{WAY} \\ $$$$\:\:\:\:\frac{\mathrm{2}}{\mathrm{x}}+\frac{\mathrm{3}}{\mathrm{x}+\mathrm{1}}+\frac{\mathrm{4}}{\mathrm{x}+\mathrm{2}}+\frac{\mathrm{5}}{\mathrm{x}+\mathrm{3}}+\frac{\mathrm{6}}{\mathrm{x}+\mathrm{4}}=\mathrm{5} \\ $$$$\mathrm{x}+\mathrm{2}=\mathrm{y}: \\ $$$$\:\:\:\:\frac{\mathrm{2}}{\mathrm{y}−\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{y}−\mathrm{1}}+\frac{\mathrm{4}}{\mathrm{y}}+\frac{\mathrm{5}}{\mathrm{y}+\mathrm{1}}+\frac{\mathrm{6}}{\mathrm{y}+\mathrm{2}}=\mathrm{5} \\ $$$$\:\:\:\:\frac{\mathrm{2}}{\mathrm{y}−\mathrm{2}}−\mathrm{1}+\frac{\mathrm{3}}{\mathrm{y}−\mathrm{1}}−\mathrm{1}+\frac{\mathrm{4}}{\mathrm{y}}−\mathrm{1}+\frac{\mathrm{5}}{\mathrm{y}+\mathrm{1}}−\mathrm{1}+\frac{\mathrm{6}}{\mathrm{y}+\mathrm{2}}−\mathrm{1}=\mathrm{0} \\ $$$$\:\:\:\frac{\mathrm{2}−\mathrm{y}+\mathrm{2}}{\mathrm{y}−\mathrm{2}}+\frac{\mathrm{3}−\mathrm{y}+\mathrm{1}}{\mathrm{y}−\mathrm{1}}+\frac{\mathrm{4}−\mathrm{y}}{\mathrm{y}}+\frac{\mathrm{5}−\mathrm{y}−\mathrm{1}}{\mathrm{y}+\mathrm{1}}+\frac{\mathrm{6}−\mathrm{y}−\mathrm{2}}{\mathrm{y}+\mathrm{2}}=\mathrm{0} \\ $$$$\:\:\:\frac{\mathrm{4}−\mathrm{y}}{\mathrm{y}−\mathrm{2}}+\frac{\mathrm{4}−\mathrm{y}}{\mathrm{y}−\mathrm{1}}+\frac{\mathrm{4}−\mathrm{y}}{\mathrm{y}}+\frac{\mathrm{4}−\mathrm{y}}{\mathrm{y}+\mathrm{1}}+\frac{\mathrm{4}−\mathrm{y}}{\mathrm{y}+\mathrm{2}}=\mathrm{0} \\ $$$$\left(\mathrm{4}−\mathrm{y}\right)\left(\frac{\mathrm{1}}{\mathrm{y}−\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{y}−\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{y}}+\frac{\mathrm{1}}{\mathrm{y}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{y}+\mathrm{2}}\right)=\mathrm{0} \\ $$$$\begin{cases}{\mathrm{4}−\mathrm{y}=\mathrm{0}\Rightarrow\mathrm{y}=\mathrm{4}\Rightarrow\mathrm{x}+\mathrm{2}=\mathrm{4}\Rightarrow\mathrm{x}=\mathrm{2}}\\{\frac{\mathrm{1}}{\mathrm{y}−\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{y}−\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{y}}+\frac{\mathrm{1}}{\mathrm{y}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{y}+\mathrm{2}}=\mathrm{0}}\end{cases} \\ $$$$\left(\frac{\mathrm{1}}{\mathrm{y}−\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{y}+\mathrm{2}}\right)+\left(\frac{\mathrm{1}}{\mathrm{y}−\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{y}+\mathrm{1}}\right)+\frac{\mathrm{1}}{\mathrm{y}}=\mathrm{0} \\ $$$$\frac{\mathrm{2y}}{\mathrm{y}^{\mathrm{2}} −\mathrm{4}}+\frac{\mathrm{2y}}{\mathrm{y}^{\mathrm{2}} −\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{y}}.\frac{\mathrm{2y}}{\mathrm{2y}}=\mathrm{0} \\ $$$$\mathrm{2y}\left(\frac{\mathrm{1}}{\mathrm{y}^{\mathrm{2}} −\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{y}^{\mathrm{2}} −\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2y}^{\mathrm{2}} }\right)=\mathrm{0} \\ $$$$\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{y}^{\mathrm{2}} −\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{y}^{\mathrm{2}} −\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2y}^{\mathrm{2}} }=\mathrm{0}\:\left[\because\mathrm{y}\neq\mathrm{0}\right] \\ $$$$\:\:\:\:\frac{\mathrm{1}}{\mathrm{y}^{\mathrm{2}} −\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{y}^{\mathrm{2}} −\mathrm{1}}=\frac{−\mathrm{1}}{\mathrm{2y}^{\mathrm{2}} } \\ $$$$\:\:\:\:\frac{\mathrm{y}^{\mathrm{2}} −\mathrm{1}+\mathrm{y}^{\mathrm{2}} −\mathrm{4}}{\left(\mathrm{y}^{\mathrm{2}} −\mathrm{4}\right)\left(\mathrm{y}^{\mathrm{2}} −\mathrm{1}\right)}=\frac{−\mathrm{1}}{\mathrm{2y}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\mathrm{2y}^{\mathrm{2}} \left(\mathrm{2y}^{\mathrm{2}} −\mathrm{5}\right)=−\left(\mathrm{y}^{\mathrm{2}} −\mathrm{4}\right)\left(\mathrm{y}^{\mathrm{2}} −\mathrm{1}\right) \\ $$$$\:\:\:\:\mathrm{4y}^{\mathrm{4}} −\mathrm{10y}^{\mathrm{2}} =−\mathrm{y}^{\mathrm{4}} +\mathrm{5y}^{\mathrm{2}} −\mathrm{4} \\ $$$$\:\:\:\:\mathrm{5y}^{\mathrm{4}} −\mathrm{15y}^{\mathrm{2}} +\mathrm{4}=\mathrm{0} \\ $$$$\:\:\:\:\mathrm{y}^{\mathrm{2}} =\frac{\mathrm{15}\pm\sqrt{\mathrm{225}−\mathrm{80}}}{\mathrm{10}}=\frac{\mathrm{15}\pm\sqrt{\mathrm{145}}}{\mathrm{10}} \\ $$$$\left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{2}} =\frac{\mathrm{15}\pm\sqrt{\mathrm{145}}}{\mathrm{10}} \\ $$$$\:\:\mathrm{x}=−\mathrm{2}\pm\sqrt{\frac{\mathrm{15}\pm\sqrt{\mathrm{145}}}{\mathrm{10}}} \\ $$$$\mathrm{x}=\mathrm{2}\:,\:−\mathrm{2}\pm\sqrt{\frac{\mathrm{15}\pm\sqrt{\mathrm{145}}}{\mathrm{10}}} \\ $$
Commented by Tawa11 last updated on 08/Oct/21
Great sir
$$\mathrm{Great}\:\mathrm{sir} \\ $$
Commented by Rasheed.Sindhi last updated on 08/Oct/21
Thanks miss!
$$\mathbb{T}\mathrm{hanks}\:\mathrm{miss}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *