Question Number 173871 by mathlove last updated on 20/Jul/22
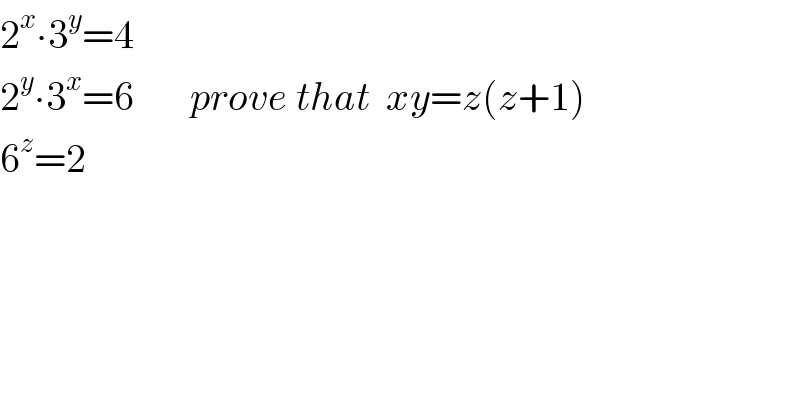
$$\mathrm{2}^{{x}} \centerdot\mathrm{3}^{{y}} =\mathrm{4} \\ $$$$\mathrm{2}^{{y}} \centerdot\mathrm{3}^{{x}} =\mathrm{6}\:\:\:\:\:\:\:{prove}\:{that}\:\:{xy}={z}\left({z}+\mathrm{1}\right) \\ $$$$\mathrm{6}^{{z}} =\mathrm{2} \\ $$
Commented by dragan91 last updated on 20/Jul/22
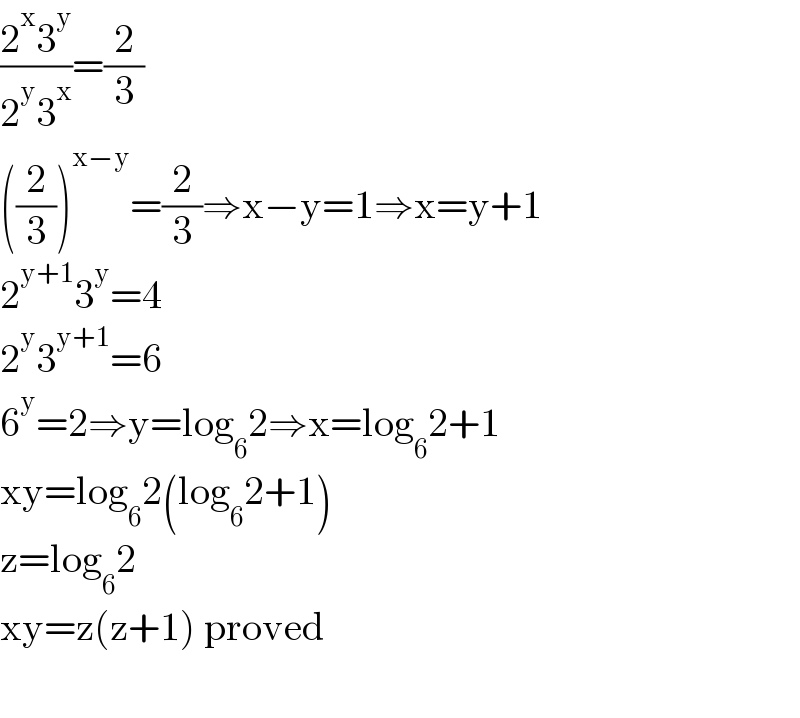
$$\frac{\mathrm{2}^{\mathrm{x}} \mathrm{3}^{\mathrm{y}} }{\mathrm{2}^{\mathrm{y}} \mathrm{3}^{\mathrm{x}} }=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{x}−\mathrm{y}} =\frac{\mathrm{2}}{\mathrm{3}}\Rightarrow\mathrm{x}−\mathrm{y}=\mathrm{1}\Rightarrow\mathrm{x}=\mathrm{y}+\mathrm{1} \\ $$$$\mathrm{2}^{\mathrm{y}+\mathrm{1}} \mathrm{3}^{\mathrm{y}} =\mathrm{4} \\ $$$$\mathrm{2}^{\mathrm{y}} \mathrm{3}^{\mathrm{y}+\mathrm{1}} =\mathrm{6} \\ $$$$\mathrm{6}^{\mathrm{y}} =\mathrm{2}\Rightarrow\mathrm{y}=\mathrm{log}_{\mathrm{6}} \mathrm{2}\Rightarrow\mathrm{x}=\mathrm{log}_{\mathrm{6}} \mathrm{2}+\mathrm{1} \\ $$$$\mathrm{xy}=\mathrm{log}_{\mathrm{6}} \mathrm{2}\left(\mathrm{log}_{\mathrm{6}} \mathrm{2}+\mathrm{1}\right) \\ $$$$\mathrm{z}=\mathrm{log}_{\mathrm{6}} \mathrm{2} \\ $$$$\mathrm{xy}=\mathrm{z}\left(\mathrm{z}+\mathrm{1}\right)\:\mathrm{proved} \\ $$$$ \\ $$
