Question Number 99789 by bemath last updated on 23/Jun/20

$$\begin{cases}{\mathrm{2}^{{x}} .\mathrm{3}^{{y}} \:=\:\mathrm{6}}\\{\mathrm{3}^{{x}} .\mathrm{4}^{{y}} \:=\:\mathrm{12}}\end{cases} \\ $$
Commented by john santu last updated on 23/Jun/20
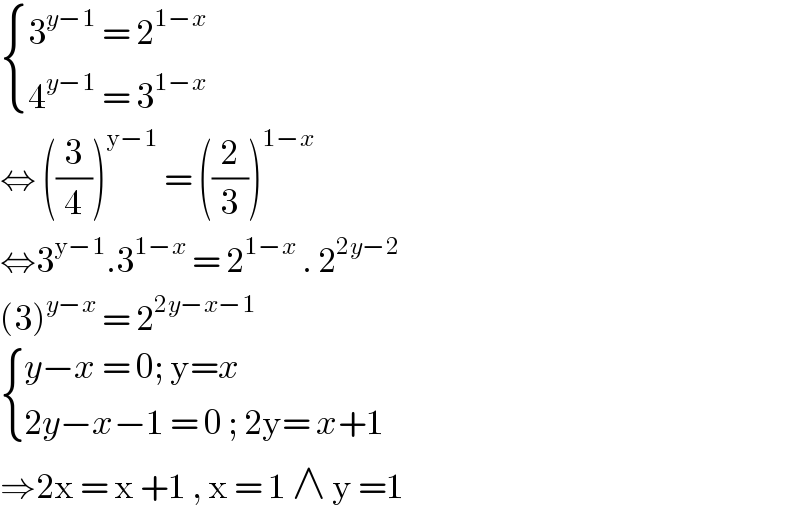
$$\begin{cases}{\mathrm{3}^{{y}−\mathrm{1}} \:=\:\mathrm{2}^{\mathrm{1}−{x}} }\\{\mathrm{4}^{{y}−\mathrm{1}} \:=\:\mathrm{3}^{\mathrm{1}−{x}} \:}\end{cases} \\ $$$$\Leftrightarrow\:\left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{y}−\mathrm{1}} \:=\:\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{1}−{x}} \\ $$$$\Leftrightarrow\mathrm{3}^{\mathrm{y}−\mathrm{1}} .\mathrm{3}^{\mathrm{1}−{x}} \:=\:\mathrm{2}^{\mathrm{1}−{x}} \:.\:\mathrm{2}^{\mathrm{2}{y}−\mathrm{2}} \\ $$$$\left(\mathrm{3}\right)^{{y}−{x}} \:=\:\mathrm{2}^{\mathrm{2}{y}−{x}−\mathrm{1}} \\ $$$$\begin{cases}{{y}−{x}\:=\:\mathrm{0};\:\mathrm{y}={x}}\\{\mathrm{2}{y}−{x}−\mathrm{1}\:=\:\mathrm{0}\:;\:\mathrm{2y}=\:{x}+\mathrm{1}}\end{cases} \\ $$$$\Rightarrow\mathrm{2x}\:=\:\mathrm{x}\:+\mathrm{1}\:,\:\mathrm{x}\:=\:\mathrm{1}\:\wedge\:\mathrm{y}\:=\mathrm{1}\: \\ $$
Commented by Dwaipayan Shikari last updated on 23/Jun/20
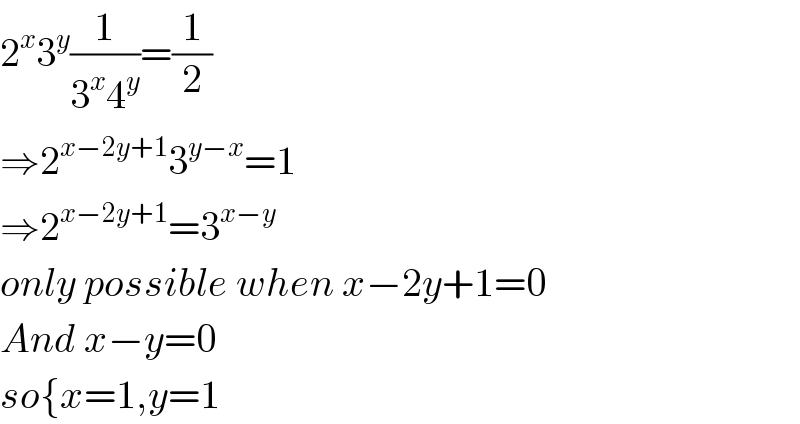
$$\mathrm{2}^{{x}} \mathrm{3}^{{y}} \frac{\mathrm{1}}{\mathrm{3}^{{x}} \mathrm{4}^{{y}} }=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2}^{{x}−\mathrm{2}{y}+\mathrm{1}} \mathrm{3}^{{y}−{x}} =\mathrm{1} \\ $$$$\Rightarrow\mathrm{2}^{{x}−\mathrm{2}{y}+\mathrm{1}} =\mathrm{3}^{{x}−{y}} \\ $$$${only}\:{possible}\:{when}\:{x}−\mathrm{2}{y}+\mathrm{1}=\mathrm{0} \\ $$$${And}\:{x}−{y}=\mathrm{0} \\ $$$${so}\left\{{x}=\mathrm{1},{y}=\mathrm{1}\right. \\ $$
