Question Number 21470 by Joel577 last updated on 24/Sep/17
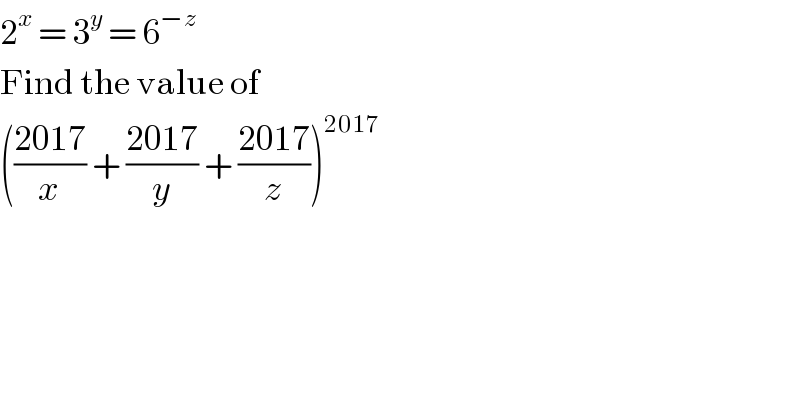
$$\mathrm{2}^{{x}} \:=\:\mathrm{3}^{{y}} \:=\:\mathrm{6}^{−{z}} \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\: \\ $$$$\left(\frac{\mathrm{2017}}{{x}}\:+\:\frac{\mathrm{2017}}{{y}}\:+\:\frac{\mathrm{2017}}{{z}}\right)^{\mathrm{2017}} \\ $$
Commented by Joel577 last updated on 24/Sep/17
![2^x = 3^y = 6^(−z) = k (k ≠ 0) 2^x = k → x =^2 log k 3^y = k → y =^3 log k 6^(−z) = k → −z =^6 log k → z =^6 log k^(−1) (((^2 log 2^(2017) )/(^2 log k)) + ((^3 log 3^(2017) )/(^3 log k)) + ((^6 log 6^(2017) )/(^6 log k^(−1) )))^(2017) = (^k log 2^(2017) +^k log 3^(2017) +^k^(−1) log 6^(2017) )^(2017) = (^k log 2^(2017) +^k log 3^(2017) −^k log 6^(2017) )^(2017) = [^k log (((2^(2017) .3^(2017) )/6^(2017) ))]^(2017) = (^k log 1)^(2017) = 0](https://www.tinkutara.com/question/Q21478.png)
$$\mathrm{2}^{{x}} \:=\:\mathrm{3}^{{y}} \:=\:\mathrm{6}^{−{z}} \:=\:{k}\:\:\:\:\:\:\:\:\:\:\:\:\:\left({k}\:\neq\:\mathrm{0}\right) \\ $$$$\mathrm{2}^{{x}} \:=\:{k}\:\:\rightarrow\:{x}\:=\:^{\mathrm{2}} \mathrm{log}\:{k} \\ $$$$\mathrm{3}^{{y}} \:=\:{k}\:\:\rightarrow\:{y}\:=\:^{\mathrm{3}} \mathrm{log}\:{k} \\ $$$$\mathrm{6}^{−{z}} \:=\:{k}\:\:\rightarrow\:\:−{z}\:=\:^{\mathrm{6}} \mathrm{log}\:{k}\:\:\rightarrow\:\:{z}\:=\:^{\mathrm{6}} \mathrm{log}\:{k}^{−\mathrm{1}} \\ $$$$ \\ $$$$\left(\frac{\:^{\mathrm{2}} \mathrm{log}\:\mathrm{2}^{\mathrm{2017}} }{\:^{\mathrm{2}} \mathrm{log}\:{k}}\:+\:\frac{\:^{\mathrm{3}} \mathrm{log}\:\mathrm{3}^{\mathrm{2017}} }{\:^{\mathrm{3}} \mathrm{log}\:{k}}\:+\:\frac{\:^{\mathrm{6}} \mathrm{log}\:\mathrm{6}^{\mathrm{2017}} }{\:^{\mathrm{6}} \mathrm{log}\:{k}^{−\mathrm{1}} }\right)^{\mathrm{2017}} \: \\ $$$$=\:\left(\:^{{k}} \mathrm{log}\:\mathrm{2}^{\mathrm{2017}} \:+\:^{{k}} \mathrm{log}\:\mathrm{3}^{\mathrm{2017}} \:+\:^{{k}^{−\mathrm{1}} } \mathrm{log}\:\mathrm{6}^{\mathrm{2017}} \right)^{\mathrm{2017}} \\ $$$$=\:\left(\:^{{k}} \mathrm{log}\:\mathrm{2}^{\mathrm{2017}} \:+\:^{{k}} \mathrm{log}\:\mathrm{3}^{\mathrm{2017}} \:−\:^{{k}} \mathrm{log}\:\mathrm{6}^{\mathrm{2017}} \right)^{\mathrm{2017}} \\ $$$$=\:\left[\:^{{k}} \mathrm{log}\:\left(\frac{\mathrm{2}^{\mathrm{2017}} .\mathrm{3}^{\mathrm{2017}} }{\mathrm{6}^{\mathrm{2017}} }\right)\right]^{\mathrm{2017}} \\ $$$$=\:\left(^{{k}} \mathrm{log}\:\mathrm{1}\right)^{\mathrm{2017}} \\ $$$$=\:\mathrm{0} \\ $$
Answered by $@ty@m last updated on 24/Sep/17

$$\mathrm{2}^{{x}} \:=\:\mathrm{3}^{{y}} \:=\:\mathrm{6}^{−{z}} ={k},\:{say} \\ $$$$\Rightarrow{k}^{\frac{\mathrm{1}}{{x}}} =\mathrm{2},\:{k}^{\frac{\mathrm{1}}{{y}}} =\mathrm{3}\:\&\:{k}^{\frac{−\mathrm{1}}{{z}}} =\mathrm{6} \\ $$$$\because\mathrm{2}×\mathrm{3}=\mathrm{6} \\ $$$$\therefore{k}^{\frac{\mathrm{1}}{{x}}} ×{k}^{\frac{\mathrm{1}}{{y}}} ={k}^{\frac{−\mathrm{1}}{{z}}} \\ $$$$\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}=\frac{−\mathrm{1}}{{z}} \\ $$$$\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}+\frac{\mathrm{1}}{{z}}=\mathrm{0} \\ $$$$\frac{\mathrm{2017}}{{x}}+\frac{\mathrm{2017}}{{y}}+\frac{\mathrm{2017}}{{z}}=\mathrm{0} \\ $$$$ \\ $$
Commented by Joel577 last updated on 26/Sep/17

$${thank}\:{you}\:{for}\:{the}\:{shortcut} \\ $$
