Question Number 185075 by aba last updated on 16/Jan/23
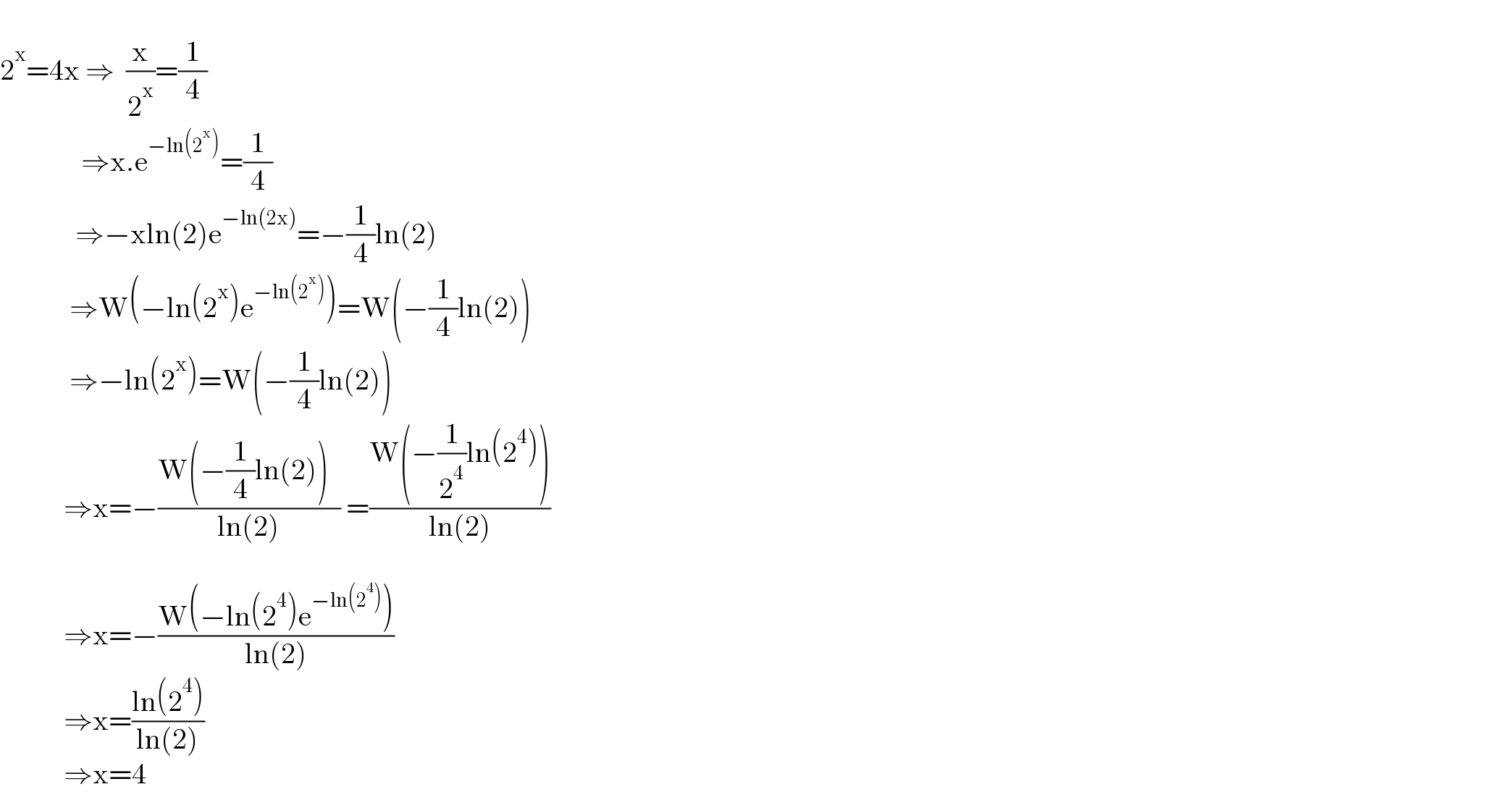
$$ \\ $$$$\mathrm{2}^{\mathrm{x}} =\mathrm{4x}\:\Rightarrow\:\:\frac{\mathrm{x}}{\mathrm{2}^{\mathrm{x}} }=\frac{\mathrm{1}}{\mathrm{4}}\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\mathrm{x}.\mathrm{e}^{−\mathrm{ln}\left(\mathrm{2}^{\mathrm{x}} \right)} =\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow−\mathrm{xln}\left(\mathrm{2}\right)\mathrm{e}^{−\mathrm{ln}\left(\mathrm{2x}\right)} =−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\left(\mathrm{2}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\mathrm{W}\left(−\mathrm{ln}\left(\mathrm{2}^{\mathrm{x}} \right)\mathrm{e}^{−\mathrm{ln}\left(\mathrm{2}^{\mathrm{x}} \right)} \right)=\mathrm{W}\left(−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\left(\mathrm{2}\right)\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow−\mathrm{ln}\left(\mathrm{2}^{\mathrm{x}} \right)=\mathrm{W}\left(−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\left(\mathrm{2}\right)\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\mathrm{x}=−\frac{\mathrm{W}\left(−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\left(\mathrm{2}\right)\right)\:\:}{\mathrm{ln}\left(\mathrm{2}\right)}\:=\frac{\mathrm{W}\left(−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{4}} }\mathrm{ln}\left(\mathrm{2}^{\mathrm{4}} \right)\right)}{\mathrm{ln}\left(\mathrm{2}\right)} \\ $$$$\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\mathrm{x}=−\frac{\mathrm{W}\left(−\mathrm{ln}\left(\mathrm{2}^{\mathrm{4}} \right)\mathrm{e}^{−\mathrm{ln}\left(\mathrm{2}^{\mathrm{4}} \right)} \right)}{\mathrm{ln}\left(\mathrm{2}\right)}\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\mathrm{x}=\frac{\mathrm{ln}\left(\mathrm{2}^{\mathrm{4}} \right)}{\mathrm{ln}\left(\mathrm{2}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\mathrm{x}=\mathrm{4} \\ $$
Commented by Frix last updated on 16/Jan/23
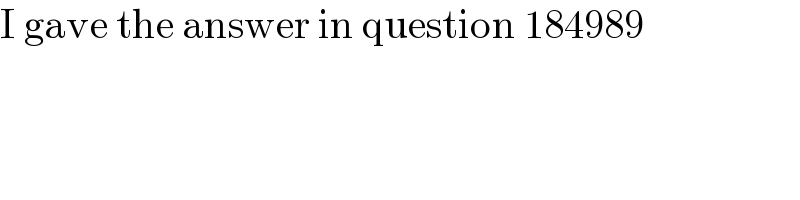
$$\mathrm{I}\:\mathrm{gave}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{in}\:\mathrm{question}\:\mathrm{184989} \\ $$
Commented by aba last updated on 16/Jan/23

$$\mathrm{yes}\:\mathrm{i}\:\mathrm{know} \\ $$
Commented by Frix last updated on 16/Jan/23
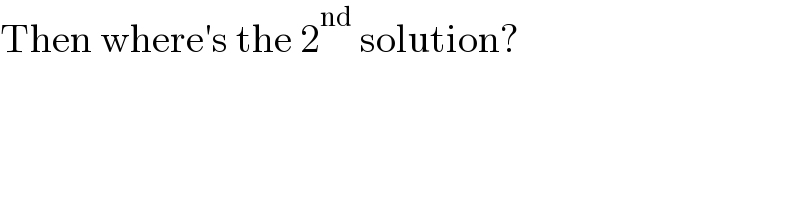
$$\mathrm{Then}\:\mathrm{where}'\mathrm{s}\:\mathrm{the}\:\mathrm{2}^{\mathrm{nd}} \:\mathrm{solution}? \\ $$
Commented by aba last updated on 16/Jan/23

$$?! \\ $$
Commented by Frix last updated on 16/Jan/23

$${x}\approx.\mathrm{309907} \\ $$
