Question Number 146532 by mathdanisur last updated on 13/Jul/21
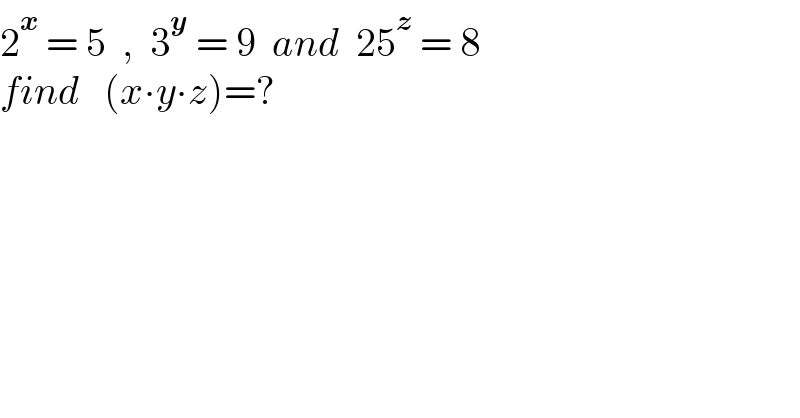
$$\mathrm{2}^{\boldsymbol{{x}}} \:=\:\mathrm{5}\:\:,\:\:\mathrm{3}^{\boldsymbol{{y}}} \:=\:\mathrm{9}\:\:{and}\:\:\mathrm{25}^{\boldsymbol{{z}}} \:=\:\mathrm{8} \\ $$$${find}\:\:\:\left({x}\centerdot{y}\centerdot{z}\right)=? \\ $$
Answered by puissant last updated on 13/Jul/21
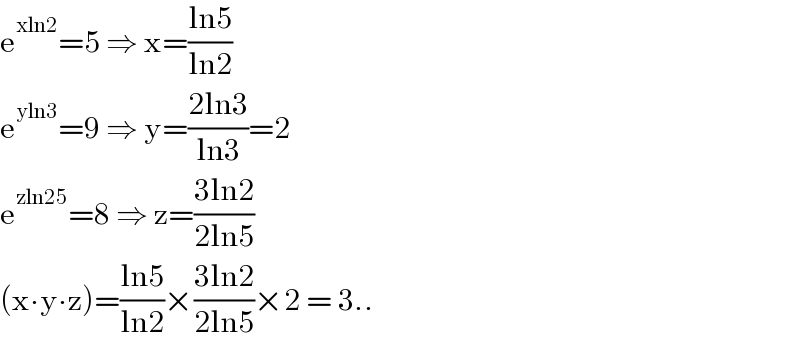
$$\mathrm{e}^{\mathrm{xln2}} =\mathrm{5}\:\Rightarrow\:\mathrm{x}=\frac{\mathrm{ln5}}{\mathrm{ln2}} \\ $$$$\mathrm{e}^{\mathrm{yln3}} =\mathrm{9}\:\Rightarrow\:\mathrm{y}=\frac{\mathrm{2ln3}}{\mathrm{ln3}}=\mathrm{2} \\ $$$$\mathrm{e}^{\mathrm{zln25}} =\mathrm{8}\:\Rightarrow\:\mathrm{z}=\frac{\mathrm{3ln2}}{\mathrm{2ln5}} \\ $$$$\left(\mathrm{x}\centerdot\mathrm{y}\centerdot\mathrm{z}\right)=\frac{\mathrm{ln5}}{\mathrm{ln2}}×\frac{\mathrm{3ln2}}{\mathrm{2ln5}}×\mathrm{2}\:=\:\mathrm{3}.. \\ $$
Commented by mathdanisur last updated on 13/Jul/21

$${cool}\:{thanks}\:{Ser} \\ $$
Answered by Rasheed.Sindhi last updated on 14/Jul/21
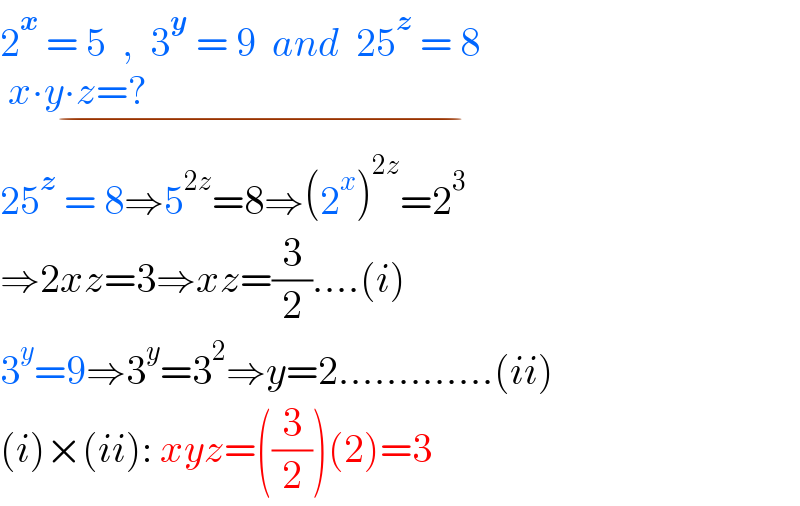
$$\mathrm{2}^{\boldsymbol{{x}}} \:=\:\mathrm{5}\:\:,\:\:\mathrm{3}^{\boldsymbol{{y}}} \:=\:\mathrm{9}\:\:{and}\:\:\mathrm{25}^{\boldsymbol{{z}}} \:=\:\mathrm{8} \\ $$$$\underset{−} {\:{x}\centerdot{y}\centerdot{z}=?\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:} \\ $$$$\mathrm{25}^{\boldsymbol{{z}}} \:=\:\mathrm{8}\Rightarrow\mathrm{5}^{\mathrm{2}{z}} =\mathrm{8}\Rightarrow\left(\mathrm{2}^{{x}} \right)^{\mathrm{2}{z}} =\mathrm{2}^{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{2}{xz}=\mathrm{3}\Rightarrow{xz}=\frac{\mathrm{3}}{\mathrm{2}}….\left({i}\right) \\ $$$$\mathrm{3}^{{y}} =\mathrm{9}\Rightarrow\mathrm{3}^{{y}} =\mathrm{3}^{\mathrm{2}} \Rightarrow{y}=\mathrm{2}………….\left({ii}\right) \\ $$$$\left({i}\right)×\left({ii}\right):\:{xyz}=\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\left(\mathrm{2}\right)=\mathrm{3} \\ $$
Commented by mathdanisur last updated on 14/Jul/21

$${thanks}\:{Ser}\:{cool} \\ $$
