Question Number 169738 by Mastermind last updated on 07/May/22

$$\mathrm{2}^{{x}} +{x}=\mathrm{11} \\ $$$${find}\:{x}? \\ $$$$ \\ $$$${Mastermind} \\ $$
Commented by mr W last updated on 08/May/22
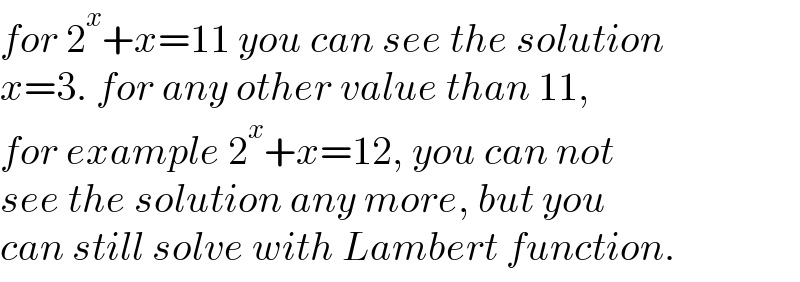
$${for}\:\mathrm{2}^{{x}} +{x}=\mathrm{11}\:{you}\:{can}\:{see}\:{the}\:{solution} \\ $$$${x}=\mathrm{3}.\:{for}\:{any}\:{other}\:{value}\:{than}\:\mathrm{11}, \\ $$$${for}\:{example}\:\mathrm{2}^{{x}} +{x}=\mathrm{12},\:{you}\:{can}\:{not} \\ $$$${see}\:{the}\:{solution}\:{any}\:{more},\:{but}\:{you} \\ $$$${can}\:{still}\:{solve}\:{with}\:{Lambert}\:{function}. \\ $$
Answered by Mathspace last updated on 07/May/22
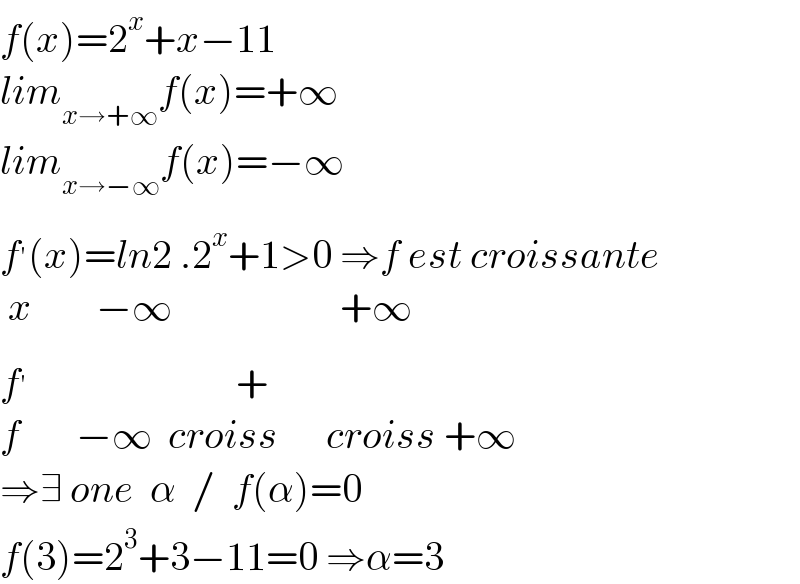
$${f}\left({x}\right)=\mathrm{2}^{{x}} +{x}−\mathrm{11} \\ $$$${lim}_{{x}\rightarrow+\infty} {f}\left({x}\right)=+\infty \\ $$$${lim}_{{x}\rightarrow−\infty} {f}\left({x}\right)=−\infty \\ $$$${f}^{'} \left({x}\right)={ln}\mathrm{2}\:.\mathrm{2}^{{x}} +\mathrm{1}>\mathrm{0}\:\Rightarrow{f}\:{est}\:{croissante} \\ $$$$\:{x}\:\:\:\:\:\:\:\:−\infty\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\infty \\ $$$${f}^{'} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+ \\ $$$${f}\:\:\:\:\:\:\:−\infty\:\:{croiss}\:\:\:\:\:\:{croiss}\:+\infty \\ $$$$\Rightarrow\exists\:{one}\:\:\alpha\:\:/\:\:{f}\left(\alpha\right)=\mathrm{0} \\ $$$${f}\left(\mathrm{3}\right)=\mathrm{2}^{\mathrm{3}} +\mathrm{3}−\mathrm{11}=\mathrm{0}\:\Rightarrow\alpha=\mathrm{3} \\ $$
Answered by Joshua24 last updated on 07/May/22
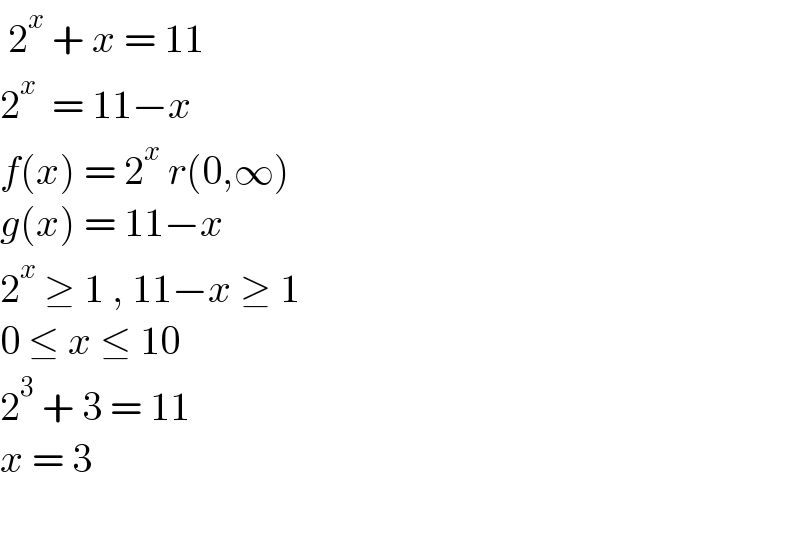
$$\:\mathrm{2}^{{x}} \:+\:{x}\:=\:\mathrm{11} \\ $$$$\mathrm{2}^{{x}} \:\:=\:\mathrm{11}−{x} \\ $$$${f}\left({x}\right)\:=\:\mathrm{2}^{{x}} \:{r}\left(\mathrm{0},\infty\right) \\ $$$${g}\left({x}\right)\:=\:\mathrm{11}−{x}\: \\ $$$$\mathrm{2}^{{x}} \:\geq\:\mathrm{1}\:,\:\mathrm{11}−{x}\:\geq\:\mathrm{1} \\ $$$$\mathrm{0}\:\leq\:{x}\:\leq\:\mathrm{10} \\ $$$$\mathrm{2}^{\mathrm{3}} \:+\:\mathrm{3}\:=\:\mathrm{11} \\ $$$${x}\:=\:\mathrm{3} \\ $$$$ \\ $$
Answered by mr W last updated on 07/May/22
![2^x +x=12 2^x =12−x 2^(12) ×2^(x−12) =(12−x) 2^(12) ×e^((x−12)ln 2) =(12−x) 2^(12) =(12−x)e^((12−x)ln 2) 2^(12) ×ln 2=[(12−x)ln 2]e^((12−x)ln 2) (12−x)ln 2=W(2^(12) ×ln 2) ⇒x=12−((W(2^(12) ×ln 2))/(ln 2)) ≈12−((6.13692882)/(ln 2))=3.146283](https://www.tinkutara.com/question/Q169741.png)
$$\mathrm{2}^{{x}} +{x}=\mathrm{12} \\ $$$$\mathrm{2}^{{x}} =\mathrm{12}−{x} \\ $$$$\mathrm{2}^{\mathrm{12}} ×\mathrm{2}^{{x}−\mathrm{12}} =\left(\mathrm{12}−{x}\right) \\ $$$$\mathrm{2}^{\mathrm{12}} ×{e}^{\left({x}−\mathrm{12}\right)\mathrm{ln}\:\mathrm{2}} =\left(\mathrm{12}−{x}\right) \\ $$$$\mathrm{2}^{\mathrm{12}} =\left(\mathrm{12}−{x}\right){e}^{\left(\mathrm{12}−{x}\right)\mathrm{ln}\:\mathrm{2}} \\ $$$$\mathrm{2}^{\mathrm{12}} ×\mathrm{ln}\:\mathrm{2}=\left[\left(\mathrm{12}−{x}\right)\mathrm{ln}\:\mathrm{2}\right]{e}^{\left(\mathrm{12}−{x}\right)\mathrm{ln}\:\mathrm{2}} \\ $$$$\left(\mathrm{12}−{x}\right)\mathrm{ln}\:\mathrm{2}=\mathbb{W}\left(\mathrm{2}^{\mathrm{12}} ×\mathrm{ln}\:\mathrm{2}\right) \\ $$$$\Rightarrow{x}=\mathrm{12}−\frac{\mathbb{W}\left(\mathrm{2}^{\mathrm{12}} ×\mathrm{ln}\:\mathrm{2}\right)}{\mathrm{ln}\:\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\approx\mathrm{12}−\frac{\mathrm{6}.\mathrm{13692882}}{\mathrm{ln}\:\mathrm{2}}=\mathrm{3}.\mathrm{146283} \\ $$
