Question Number 58862 by George Mark Samuel last updated on 01/May/19
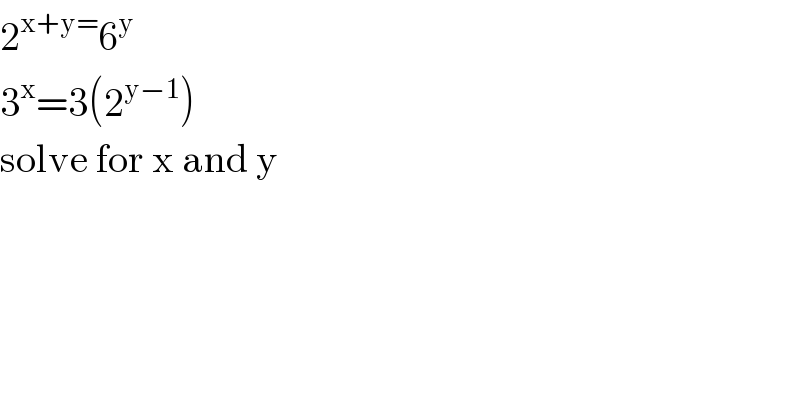
$$\mathrm{2}^{\mathrm{x}+\mathrm{y}=} \mathrm{6}^{\mathrm{y}} \\ $$$$\mathrm{3}^{\mathrm{x}} =\mathrm{3}\left(\mathrm{2}^{\mathrm{y}−\mathrm{1}} \right) \\ $$$$\mathrm{solve}\:\mathrm{for}\:\mathrm{x}\:\mathrm{and}\:\mathrm{y} \\ $$
Answered by MJS last updated on 01/May/19
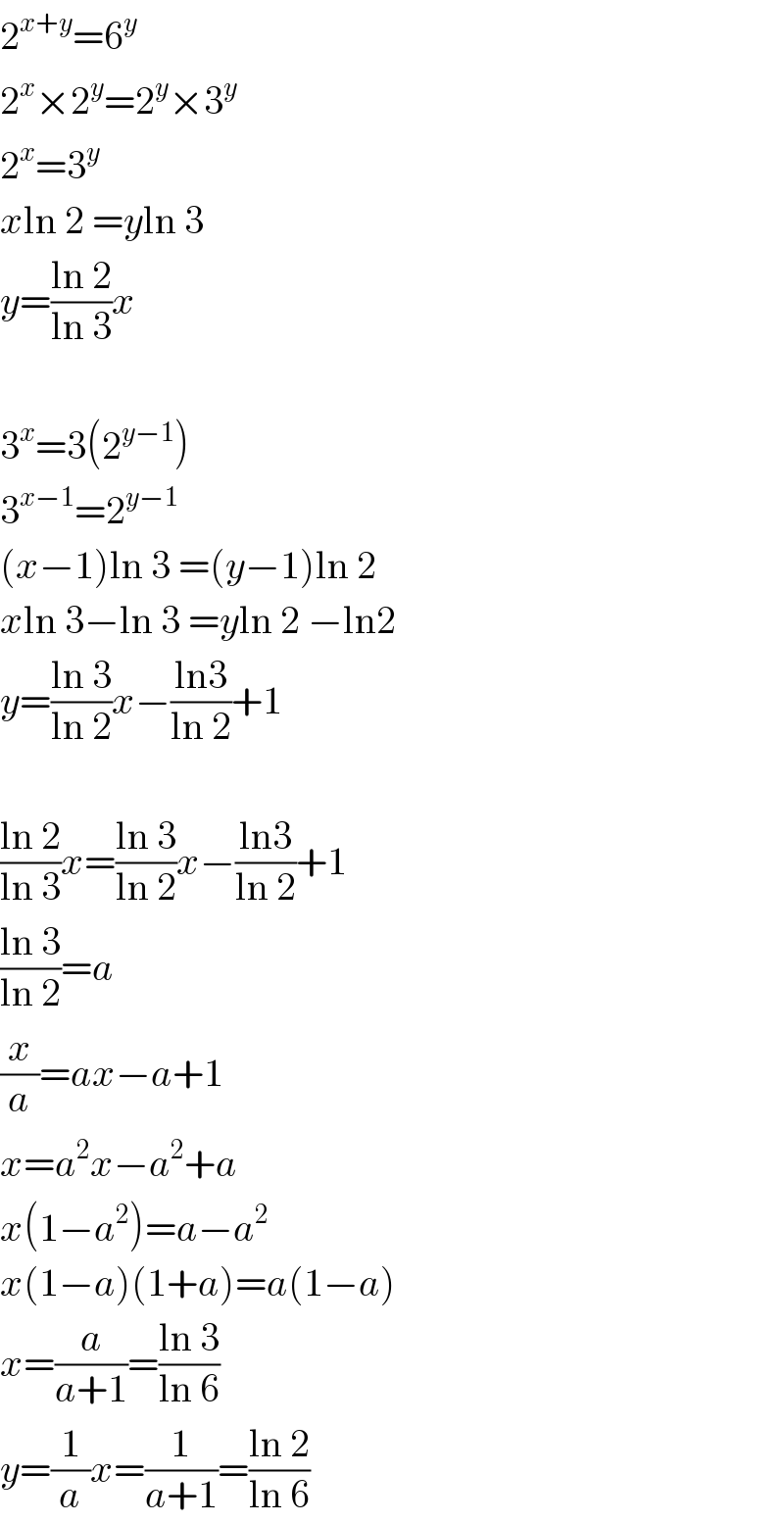
$$\mathrm{2}^{{x}+{y}} =\mathrm{6}^{{y}} \\ $$$$\mathrm{2}^{{x}} ×\mathrm{2}^{{y}} =\mathrm{2}^{{y}} ×\mathrm{3}^{{y}} \\ $$$$\mathrm{2}^{{x}} =\mathrm{3}^{{y}} \\ $$$${x}\mathrm{ln}\:\mathrm{2}\:={y}\mathrm{ln}\:\mathrm{3} \\ $$$${y}=\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{ln}\:\mathrm{3}}{x} \\ $$$$ \\ $$$$\mathrm{3}^{{x}} =\mathrm{3}\left(\mathrm{2}^{{y}−\mathrm{1}} \right) \\ $$$$\mathrm{3}^{{x}−\mathrm{1}} =\mathrm{2}^{{y}−\mathrm{1}} \\ $$$$\left({x}−\mathrm{1}\right)\mathrm{ln}\:\mathrm{3}\:=\left({y}−\mathrm{1}\right)\mathrm{ln}\:\mathrm{2} \\ $$$${x}\mathrm{ln}\:\mathrm{3}−\mathrm{ln}\:\mathrm{3}\:={y}\mathrm{ln}\:\mathrm{2}\:−\mathrm{ln2} \\ $$$${y}=\frac{\mathrm{ln}\:\mathrm{3}}{\mathrm{ln}\:\mathrm{2}}{x}−\frac{\mathrm{ln3}}{\mathrm{ln}\:\mathrm{2}}+\mathrm{1} \\ $$$$ \\ $$$$\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{ln}\:\mathrm{3}}{x}=\frac{\mathrm{ln}\:\mathrm{3}}{\mathrm{ln}\:\mathrm{2}}{x}−\frac{\mathrm{ln3}}{\mathrm{ln}\:\mathrm{2}}+\mathrm{1} \\ $$$$\frac{\mathrm{ln}\:\mathrm{3}}{\mathrm{ln}\:\mathrm{2}}={a} \\ $$$$\frac{{x}}{{a}}={ax}−{a}+\mathrm{1} \\ $$$${x}={a}^{\mathrm{2}} {x}−{a}^{\mathrm{2}} +{a} \\ $$$${x}\left(\mathrm{1}−{a}^{\mathrm{2}} \right)={a}−{a}^{\mathrm{2}} \\ $$$${x}\left(\mathrm{1}−{a}\right)\left(\mathrm{1}+{a}\right)={a}\left(\mathrm{1}−{a}\right) \\ $$$${x}=\frac{{a}}{{a}+\mathrm{1}}=\frac{\mathrm{ln}\:\mathrm{3}}{\mathrm{ln}\:\mathrm{6}} \\ $$$${y}=\frac{\mathrm{1}}{{a}}{x}=\frac{\mathrm{1}}{{a}+\mathrm{1}}=\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{ln}\:\mathrm{6}} \\ $$
