Question Number 189639 by mnjuly1970 last updated on 19/Mar/23
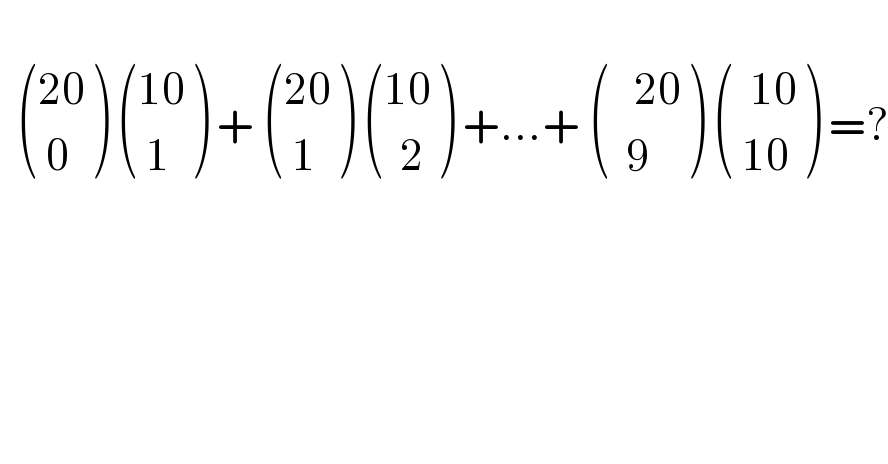
$$ \\ $$$$\:\:\begin{pmatrix}{\mathrm{20}}\\{\:\mathrm{0}}\end{pmatrix}\:\begin{pmatrix}{\mathrm{10}}\\{\:\mathrm{1}}\end{pmatrix}\:+\:\begin{pmatrix}{\mathrm{20}}\\{\:\mathrm{1}}\end{pmatrix}\:\begin{pmatrix}{\mathrm{10}}\\{\:\:\mathrm{2}}\end{pmatrix}\:+…+\:\begin{pmatrix}{\:\:\:\mathrm{20}}\\{\:\:\mathrm{9}}\end{pmatrix}\:\begin{pmatrix}{\:\:\mathrm{10}}\\{\:\mathrm{10}}\end{pmatrix}\:=? \\ $$$$ \\ $$
Commented by cortano12 last updated on 21/Mar/23

$$\:=\:\begin{pmatrix}{\mathrm{30}}\\{\:\:\mathrm{9}}\end{pmatrix}\:=\frac{\mathrm{30}.\mathrm{29}.\mathrm{28}.\mathrm{27}.\mathrm{26}.\mathrm{25}.\mathrm{24}.\mathrm{23}.\mathrm{22}}{\mathrm{9}.\mathrm{8}.\mathrm{7}.\mathrm{6}.\mathrm{5}.\mathrm{4}.\mathrm{3}.\mathrm{2}.\mathrm{1}} \\ $$$$\:\:\:\:=\:\mathrm{14},\mathrm{307},\mathrm{150} \\ $$
Answered by mr W last updated on 21/Mar/23
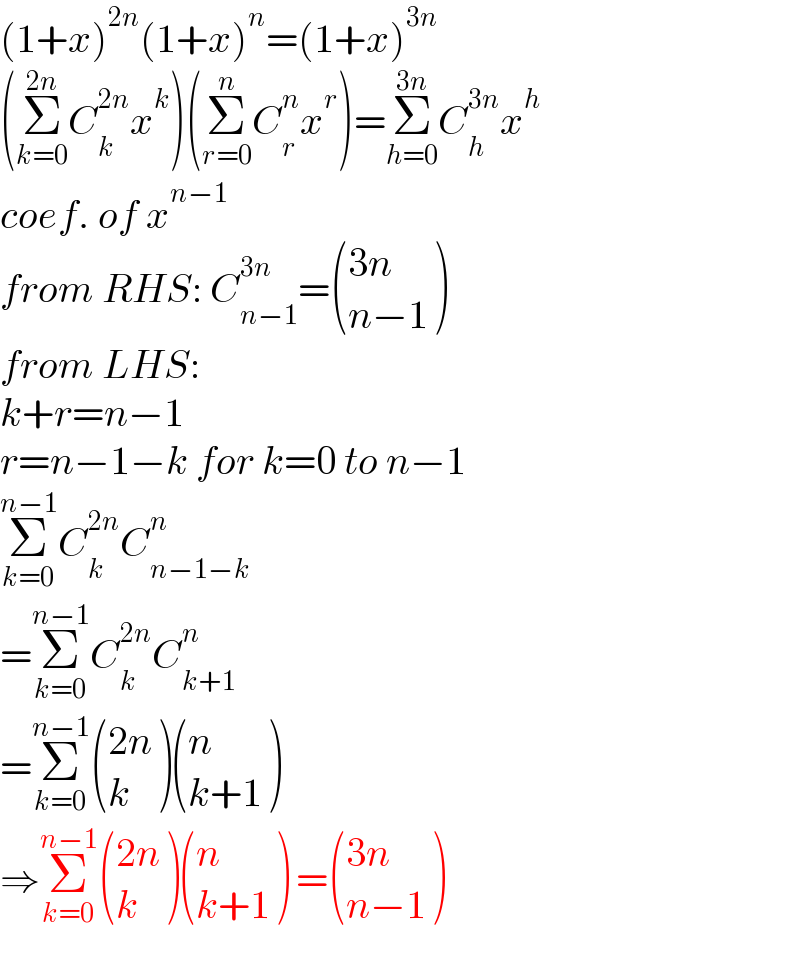
$$\left(\mathrm{1}+{x}\right)^{\mathrm{2}{n}} \left(\mathrm{1}+{x}\right)^{{n}} =\left(\mathrm{1}+{x}\right)^{\mathrm{3}{n}} \\ $$$$\left(\underset{{k}=\mathrm{0}} {\overset{\mathrm{2}{n}} {\sum}}{C}_{{k}} ^{\mathrm{2}{n}} {x}^{{k}} \right)\left(\underset{{r}=\mathrm{0}} {\overset{{n}} {\sum}}{C}_{{r}} ^{{n}} {x}^{{r}} \right)=\underset{{h}=\mathrm{0}} {\overset{\mathrm{3}{n}} {\sum}}{C}_{{h}} ^{\mathrm{3}{n}} {x}^{{h}} \\ $$$${coef}.\:{of}\:{x}^{{n}−\mathrm{1}} \\ $$$${from}\:{RHS}:\:{C}_{{n}−\mathrm{1}} ^{\mathrm{3}{n}} =\begin{pmatrix}{\mathrm{3}{n}}\\{{n}−\mathrm{1}}\end{pmatrix} \\ $$$${from}\:{LHS}:\: \\ $$$${k}+{r}={n}−\mathrm{1} \\ $$$${r}={n}−\mathrm{1}−{k}\:{for}\:{k}=\mathrm{0}\:{to}\:{n}−\mathrm{1} \\ $$$$\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}{C}_{{k}} ^{\mathrm{2}{n}} {C}_{{n}−\mathrm{1}−{k}} ^{{n}} \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}{C}_{{k}} ^{\mathrm{2}{n}} {C}_{{k}+\mathrm{1}} ^{{n}} \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\begin{pmatrix}{\mathrm{2}{n}}\\{{k}}\end{pmatrix}\begin{pmatrix}{{n}}\\{{k}+\mathrm{1}}\end{pmatrix} \\ $$$$\Rightarrow\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\begin{pmatrix}{\mathrm{2}{n}}\\{{k}}\end{pmatrix}\begin{pmatrix}{{n}}\\{{k}+\mathrm{1}}\end{pmatrix}\:=\begin{pmatrix}{\mathrm{3}{n}}\\{{n}−\mathrm{1}}\end{pmatrix} \\ $$
